Question

What is `lim_(x to pi) (sin3x)/(sin2x)`?

Answer 1

`-3/2`

Explanation:

`lim_(x->pi)(sin3x)/(sin2x)-> 0/0`

So we can use L'Hopital's rule:

`d/dxsin3x = 3cos3x`

`d/dxsin2x=2cos2x`

`thereforelim_(x->pi)(sin3x)/(sin2x)=lim_(x-> pi)(3cos3x)/(2cos2x)`

`=(3cos(3pi))/(2cos(2pi))=(3*(-1))/(2*1)=-3/2`

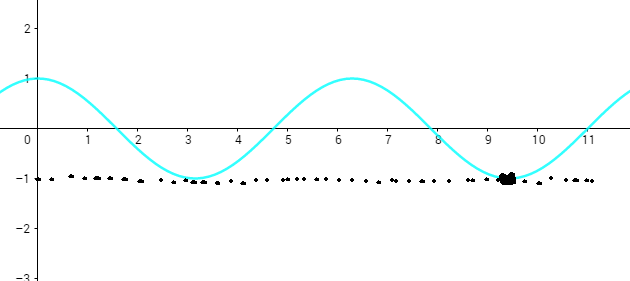
This is in agreement with the graph of the function:

graph{(sin(3x))/(sin(2x)) [-7.31, 12.69, -5.16, 4.84]}

Clicking on the graph at the right location, it can be seen that at `x=pi`, `y=-3/2=-1.5`

Answer 2

`lim_(x to pi) (sin3x)/(sin2x)=-3/2`

Explanation:

`lim_(x to pi) (sin3x)/(sin2x)=_(D.L.H)^((0/0))`

`lim_(x to pi) ((3x)'cos3x)/((2x)'cos2x)` `=`

`3/2lim_(x to pi) (cos3x)/(cos2x)` `=`

`3/2*(cos3pi)/(cos2pi)` `=`

`-3/2`

because
`cos3pi=-1`
`cos2pi=1`

Answer 3

`lim_(x->pi)(sin3x)/(sin2x)=-3/2`

Explanation:

Here's a method without using l'Hopital's rule. I personally feel this method to be more challenging and fun.

`sin3x=sin(2x+x)=sin2xcosx+cos2xsinx=`

`2sinxcos^2x+(cos^2x-sin^2x)sinx=`

`2sinxcos^2x+cos^2xsinx-sin^3x=`

`sinx(2cos^2x-sin^2x+cos^2x)=`

`sinx(2cos^2x-sin^2x+1-sin^2x)=`

`sinx(2cos^2x-2sin^2x+1)=`

`sinx(2cos2x+1)`

`sin2x=2sinxcosx`

So `(sin3x)/(sin2x)=(sinx(2cos2x+1))/(2sinxcosx)=(2cos2x+1)/(2cosx)`

And `lim_(x->pi)(sin3x)/(sin2x)=lim_(x->pi)(2cos2x+1)/(2cosx)=(2cos2pi+1)/(2cospi)=-3/2`