Question

How do you differentiate `(x-1)/sqrt(6-x)`?

Answer 1

By using quotient rule:

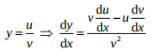
Explanation:

Let `u=x-1` and `v=sqrt(6-x)`
`(du)/dx = 1` and `(dv)/dx = -1/2(6-x)^(-1/2)`

Plugging this into the formula, you get:

Step one:

`dy/dx = ((sqrt(6-x))(1)-(x-1)(-1/2)(6-x)^(-1/2))/((sqrt(6-x))^2)`

Step two: simplify

`dy/dx = ((sqrt(6-x))+(1/2)(x-1)(6-x)^(-1/2))/(6-x)`

Step three: split numerator

`dy/dx = (sqrt(6-x))/(6-x) + ((1/2)(x-1)(6-x)^(-1/2))/(6-x)`

Step Four: combine the `(6-x)` terms using exponent rules

`dy/dx = (6-x)^(-1/2) + (1/2)(x-1)(6-x)^(-3/2)`

Step Five: write with positive exponents only

`dy/dx = 1/((6-x)^(1/2)) + (x-1)/(2(6-x)^(3/2))`

There may be other ways to further simplify the derivative, but this is what I would have done.

For future questions like this, use https://www.derivative-calculator.net/ It gives you the step by step process for any differentiation.