Pg 24, q51. How do I figure this out? thanks
2 Answers
Explanation:
Consider for the
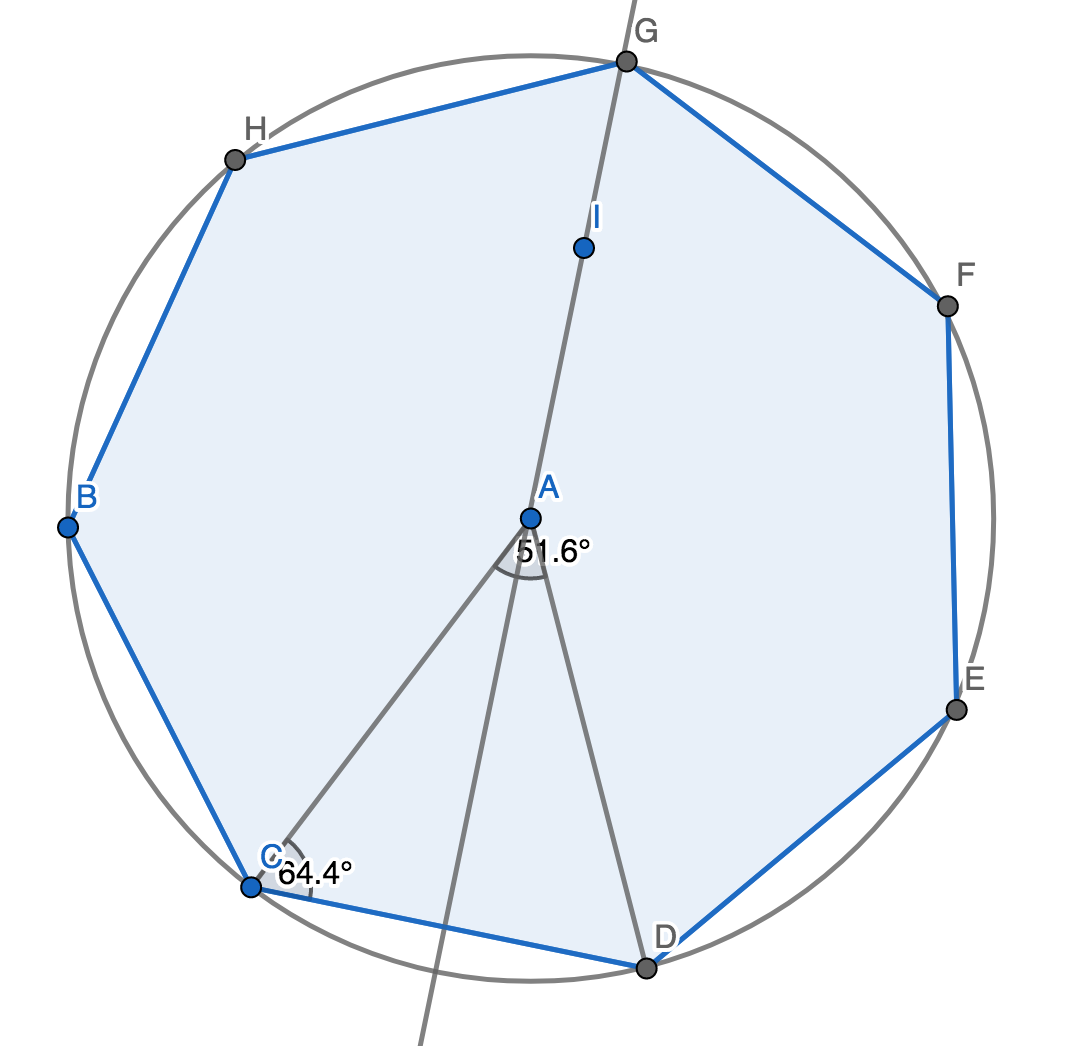
For symmetry reasons, the area of the polygon is
Moreover the triangle is isosceles and the angle at the top is:
so that we can see that the height of the triangle is:
while the length of the side is:
The area of the triangle is then:
and the area of the polygon is:
If we write this as:
We can see that as
See below
Explanation:
The regular polygons are able to be split into equal isosceles triangles.
The number of these triangles is equal to the number of sides in the polygon, so for
The area for one of these triangles is equal to
N.B. If an equation uses
So, we know have an area for one triangle,
However, we need to total area.
n=5:
n=6:
n=7:
n=8:
In general, as the value of
With radians:
With degrees:
This effect can be explored further, using just a value for the angle, here. Keep in mind that the notes sections don't allow for formatting, i.e. fractions.


