Question #75d32
1 Answer
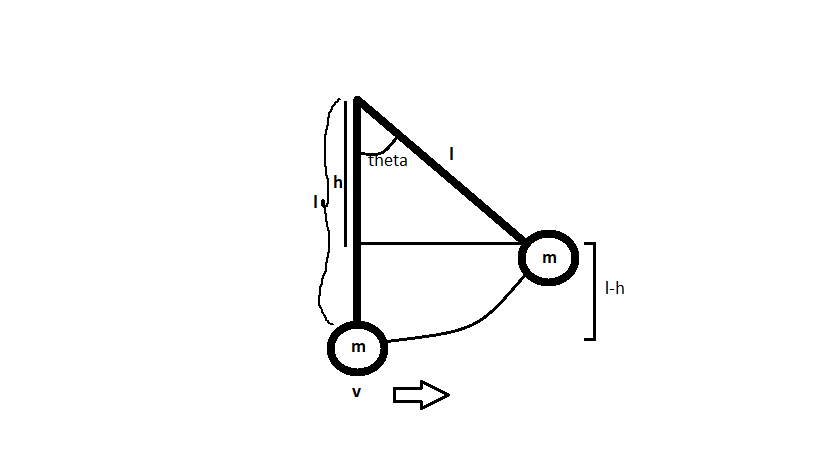
See the diagram made,where a pendulum of string length
So,vertically it has shifted a distance of
Now,
Now, in its pathway,energy will be conserved.
So,at its mean position,total energy is kinetic energy i.e
And, at the highest point,its total energy is purely potential energy i.e
So,equating both we get,
ALTERNATIVELY,
Suppose, a particle in S.H.M follows the equation,
For,a simple pendulum,
So, its velocity equation will be,
From 1 we can say
So,putting the value of
Now, for the given equation,
So,putting
This the equation of the velocity of a particle under SHM at its mean position.
Now, see maximum value of
That means,velocity is the maximum in the mean position as well.

