Question

How many moles of each atom are present in a `1.01*g` mass of antifreeze, `C_3H_6O_3`?

Answer 1

Got a Periodic Table...?

Explanation:

`"Molar quantity"="Moles of stuff"/"Molar mass of stuff"`

And the mole is just a very large number, like a dozen or a gross. For the first problem, we simply calculate the molar mass of sodium chloride.... The Periodic Table tells you that the molar mass of carbon is `12.01*g*mol^-1`, and that of hydrogen is `1.00794*g*mol^-1` and that of oxygen is `16.00*g*mol^-1`...and we simply add these together to get the molar mass of `C_3H_6O_3`....

`"Molar mass of "C_3H_6O_3-=(3xx12.011+6xx1.00794+3xx16.00)*g*mol^-1=90.0*g*mol^-1`.

The table specifies a `1.01*g` mass of antifreeze, and so we take the defining quotient....

`"Moles of"` `C_3H_6O_3-=(1.01*g)/(90.0*g*mol^-1)=0.0112*mol`.

All I am doing is adding up the masses of each mole of atoms, and then taking a quotient. Do you follow?

Answer 2

Explanation:

First, let's figure out the molar mass for everything!
Molar mass is just the mass of `1` mole of that particular compound. To find it, we add the individual element molar masses.

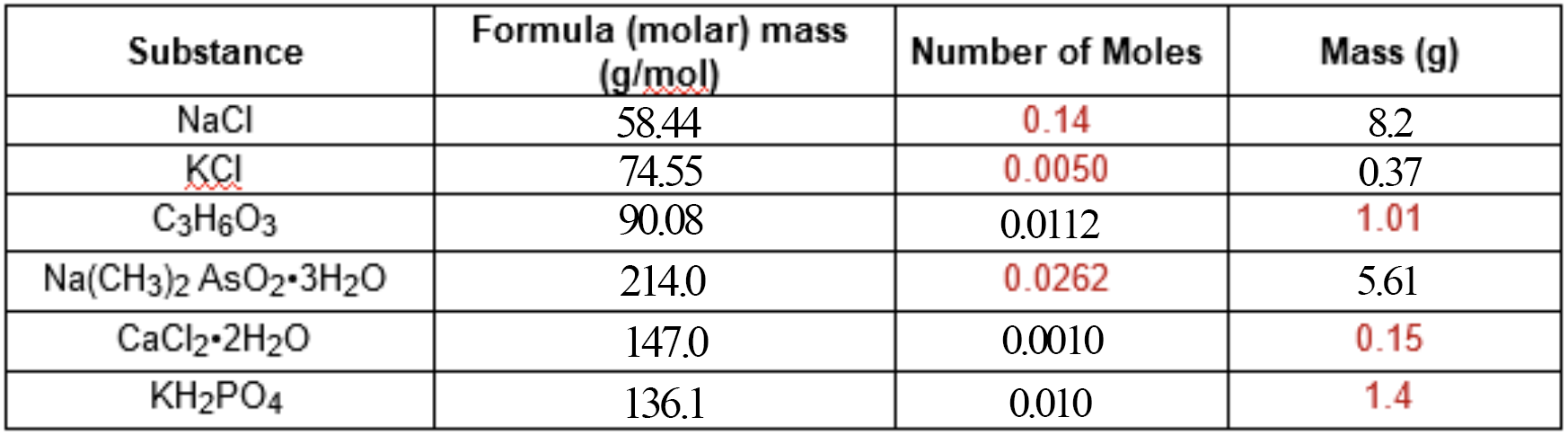
1. `NaCl` is `"58.44 g/mol"`, because `Na + Cl = "22.99g + 35.45g" = "58.44g"`

2. `KCl` is `"74.55 g/mol"`.

3. `C_3H_6O_3` is `"90.08 g/mol"`, because `3*C + 6*H + 3*O = 3*"12.01g" + 6*"1.008g" + 3*"16.00g"= "90.08g"`

4. `Na(CH_3)_2AsO_2*3H_2O` is `"214.0 g/mol"`. It looks intimidating, but it's the same principle—we just need to add up the individual element masses! :)
   `(Na + 2*(C+3*H) + As + 2*O) + 3*(2*H+O) = (22.99 + 2*(12.01+3*1.008) + 74.92 + 2*16.00) + 3*(2*1.008+16.00)`

5. `CaCl_2*2H_2O` is `"147.0 g/mol"`, because, again, we just need to add the molar mass of `CaCl_2`, which is `111.0`, with the mass of `2` moles of water, which is `"36.04g"`

6. `KH_2PO_4` is `"136.1 g/mol"`.

Now, let's go over to the second column.
To determine the number of moles from any given mass, just divide the mass of that sample by the mass of `1` mole.

`"number of moles" = "mass of sample"/"mass of 1 mole"`

• `"1.01g"` of `C_3H_6O_3` would be
  `1.01/90.08 = "0.0112 moles"`

• `"0.15 g"` of `CaCl_2*2H_2O` would be
  `0.15/147.0 = "0.0010 moles"`

• `"1.4 g"` of `KH_2PO_4` would be
  `1.4/136.1 = "0.010 moles"`

Let's fill in the second column.

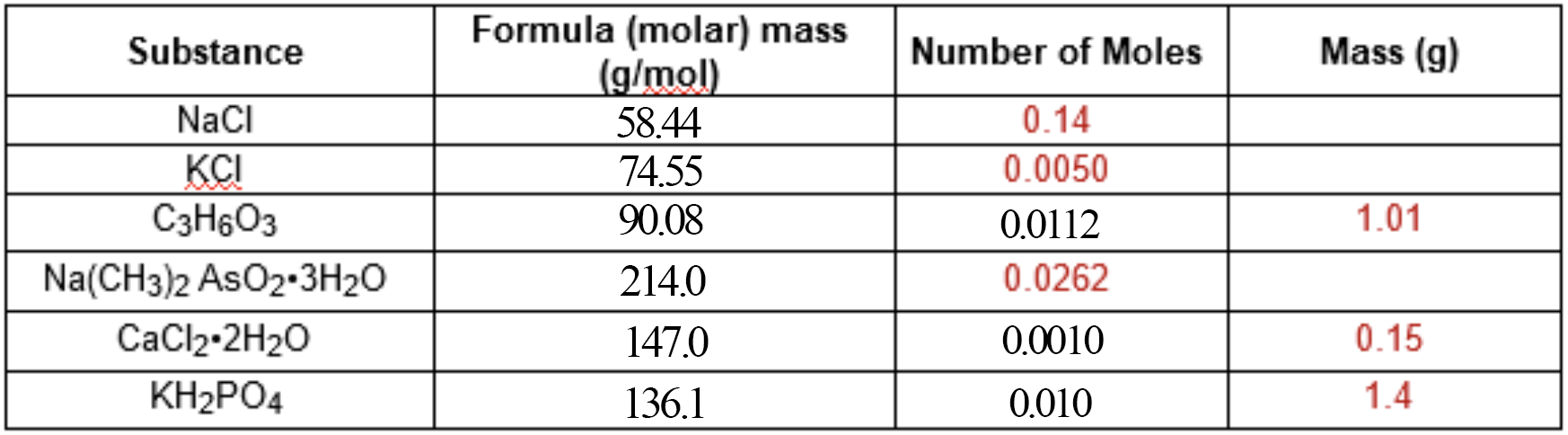
Finally, the third column.
We used this equation for converting from mass to moles:

`"number of moles" = "mass of sample"/"mass of 1 mole"`

We can slightly alter this equation to make it suit column `3`, `"mass of sample" = "number of moles"*"mass of 1 mole"`

• `"0.14 moles"` of `NaCl` is
  `0.14 * 58.44 = "8.2g"`

• `"0.0050 moles"` of `KCl` is
  `0.0050 * 74.55 = "0.37g"`

• `"0.0262 moles"` of `Na(CH_3)_2AsO_2*3H_2O` is
  `0.0262 * 214.0 = "5.61g"`