Question #75911
4 Answers
Zeroes at
Explanation:
What I have in blue, we can multiply it using
-
Multiply the first terms
#(2x and 2x)# to get#4x^2# -
The outside terms
#(2x and -5)# to get#-10x# -
The inner terms
#(-5 and 2x)# to get#-10x# -
The last terms
#(-5 and -5)# to get#25#
Combining like terms, we get:
Now, at this point, there are a few things we could do, however the easiest may be to use the quadratic formula.
Quadratic Formula:
When a quadratic equation is in standard form, it is of the form:
Now, let's plug into the quadratic formula:
Let's simplify now:
Adding the terms in the radical:
Further simplifying the radical:
All of these terms have a 10 in common, so we can divide each by 10.
We'll have 2 solutions:
1)
2)
Our two zeroes (solutions to this equation) are
Explanation:
using FOIL method to expand brackets:
collect like terms:
factorise by grouping:
find two numbers that multiply to make the product of the first and last numbers, and add to make the middle number.
make the second number (the coefficient of
find common factors in each expression:
add these together and simplify with a common factor:
then solve for
this is the graph:
the two graphs meet where
Explanation:
We need to combine the
But
Notice that 5 will divide exactly into all the values on the left of the equals sign. So divide all of both sides by 5.
Note that
I chose to use the formula
Where
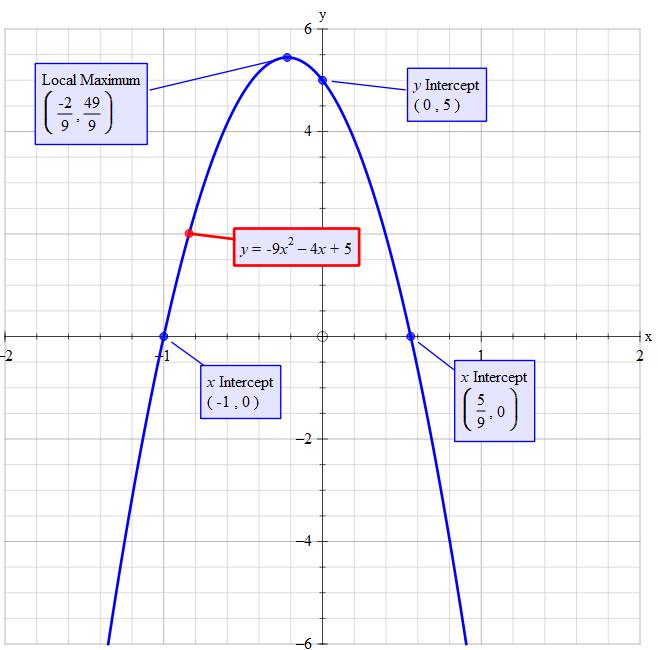
Explanation:
#(2x-5)^2-49x^2" is a "color(blue)"difference of squares"#
#•color(white)(x)a^2-b^2=(a-b)(a+b)#
#"here "a=2x-5" and "b=7x#
#rArr(2x-5)^2-49x^2#
#=(2x-5-7x)(2x-5+7x)#
#=(-5x-5)(9x-5)#
#rArr(-5x-5)(9x-5)=0#
#"equate each factor to zero and solve for x"#
#-5x-5=0rArrx=-1#
#9x-5=0rArrx=5/9#



