As the gradient is fixed this is a strait line question.
#color(blue)("Step 1")#
Consider the standardised form #y=mx+c#
where slope (gradient) #->m=3/5# as given. So we now have
#color(green)(y=color(red)(m)x+c color(white)("dddd")->color(white)("dddd")y=color(red)(3/5)x+c)#
#color(blue)("Step 2")#
Set the given point as #P_1->(x,y)=(2,-4)#
We know that the line passes through this point so we can substitute those values into the equation to determine #c#
#y=3/5x+c color(white)("dddd")->color(white)("dddd")-4=3/5(2)+c#
#color(white)("ddddddddddddd")-> color(white)("dddd")-4=6/5+c#
Subtract # color(red)(6/5) # from both sides
#color(green)(-4color(white)("d")=color(white)("d")6/5+c color(white)("ddd")->color(white)("ddd")-4color(red)(-6/5)color(white)("d")=color(white)("d")6/5color(red)(-6/5)+c#
#color(green)(color(white)("ddddddddddddddd")->color(white)("dddd")-26/5color(white)("dd")=color(white)("ddd")0color(white)("dd")+c#
#color(blue)("Putting it all together")#
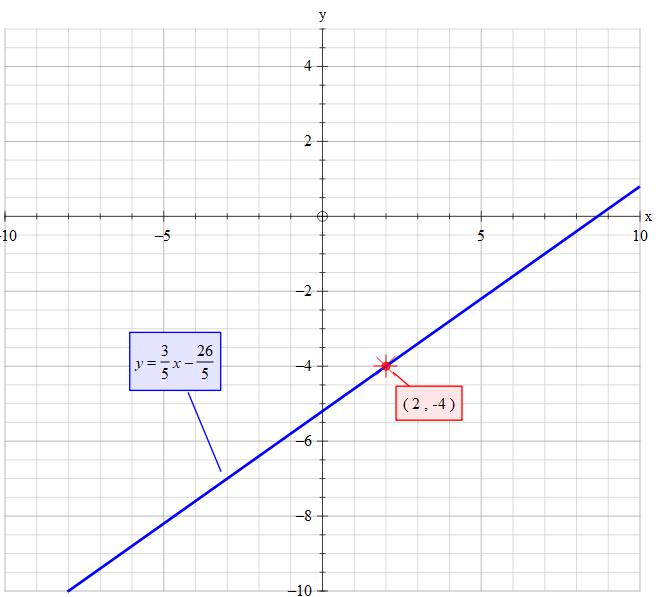
#color(white)("ddddddddddddddddd") ul(bar(|color(white)(2/2)y=3/5x-26/5color(white)(2)|))#
Note that this is the same as: #-3x+5y=-26#
or if you prefer #color(white)("dddddddddddd")3x-5y=+26#
Which are a different standardised form.