Question

What is the critical value of μs?

A woman attempts to push a box of books that has mass m up a ramp inclined at an angle α above the horizontal. The coefficients of friction between the ramp and the box are μs and μk. The force F applied by the woman is horizontal.
a.If μs is greater than some critical value, the woman cannot start the box moving up the ramp no matter how hard she pushes. Calculate this critical value μs.

b. Assume that μs is less than this critical value. What magnitude of force must the woman apply to keep the box moving up the ramp at constant speed?

Answer 1

`mu_s = cottheta`
`F= (Mg(1+mu_scottheta))/(cottheta - mu_s)`

Explanation:

A good approach to solve this problem is to represent all forces involved in a Free Body Diagram as show below:

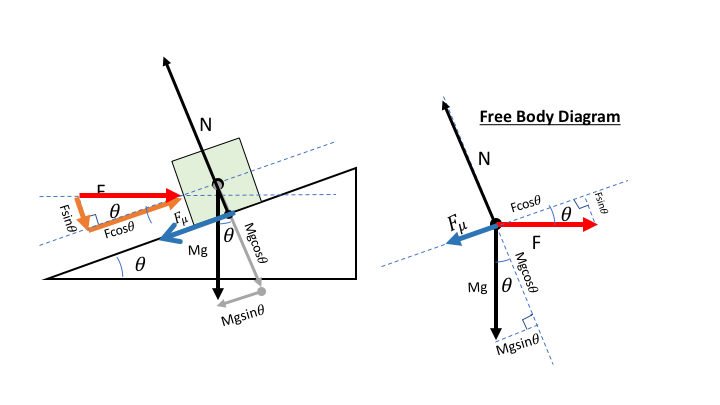
The FBD on the right shows that three are 4 forces acting on the body, horizontal F pushed by the lady, the weight due to gravity, the normal force, and the normal force induced friction. Resolve all forces, i.e., Mg and F, into components that are parallel or perpendicular to the inclined plane. We then use these components to solve `F_"net" =ma` in directions that are parallel and then perpendicular to the inclined plane

Since the block either goes up or down inclined plane, the net force is effective acting parallel to the inclined plane.

The minimum F required to initiate a motion while the box is initially at rest uphill force component (LHS of the equation below) to balance the downhill force components (RHS). Hence

`Fcostheta = mgsintheta+ mu_sN ...............................Eq (1)`

Because there are two forces pushing the box into the inclined plane and that # F_"net" =0 in the perpendicular direction,

`N - Mgcostheta -Fsintheta=0`

`rArr N = Mgcostheta + Fsintheta.......................Eq.(2)`

Substitute Eq.2 into Eq. 1,

`Fcostheta = mgsintheta+ mu_s(Mgcostheta+Fsintheta)`

Collect term to solve for F

`Fcostheta - mu_sFsintheta= Mgsintheta+mu_sMgcostheta`

`F(costheta - mu_ssintheta)= Mgsintheta+mu_sMgcostheta`

`F= (Mgsintheta+mu_sMgcostheta)/(costheta - mu_ssintheta)`

Factor out `Mg or sintheta` and then simply the equation

`F= (Mgcancel(sintheta)(1+mu_scostheta/sintheta))/(cancel(sintheta)(costheta/sintheta- mu_s))=(Mg(1+mu_scottheta))/(cottheta - mu_s) ...Eq (3)`

Obviously, when numerator becomes zero, `F` becomes infinitely large.

Hence the critical value of static coefficient is

`mu_s = cottheta`.................................Eq.(4)

If `cot theta gt mu_s` , the required force can be readily calculated from Eq.3 above.

If `cot theta lt mu_s` , the box will slides downhill instead.