Find the ratio in which the staight line 5x+4y=4 divides the join of (4,5) and (7,-1)?

2 Answers
HighwireAct
Feb 17, 2018

#1/3#

Explanation:

There are a few things we'll need to establish before we can find the requested ratio. If we want a ratio between two line segments, we'll obviously need two line segments, and in order to have two line segments, we'll need three points. Two points - #A(4,5)# and #B(7,-1)# - have been provided, but we'll need to find the third by determining where the line #5x+4x=4# and #AB# intersect.

Before we can do that, though, we'll need to find the equation for #AB#. If you'll recall, a line is defined by some constant rate of change - its slope, #m#, were

#m=(Deltay)/(Deltax)#

Here, we can take our two points to find that

#m=(-1-5)/(7-4)=-6/3=-2#

With that in place, we can derive the general form of the line's equation by fixing one point in place - say, #A(4,5)# - and letting the other vary (i.e. it can be any arbitrary point #(x,y)# on the line):

#-2=(y-5)/(x-4)#

#-2(x-4)=y-5#
#-2x+8=y-5#
#13=y+2x#
#2x+y=13#

Now that we have that equation, we can set up a system and solve for the intersection of the two:

#(1)\ 5x+4y=4#
#(2) \ 2x+y=13#

Here, I'll solve by substition by first manipulating the second equation to get:

#y=13-2x#

which, substituting into #(1)#:

#5x+4(13-2x)=4#
#5x+52-8x=4#
#52-3x=4#
#48=3x#
#x=16#

Solving for #y#:

#y=13-2(16)#
#y=13-32#
#y=-19#

So our point of intersection is #C(16,-19)#.

For a feel as to what our picture looks like at this point:

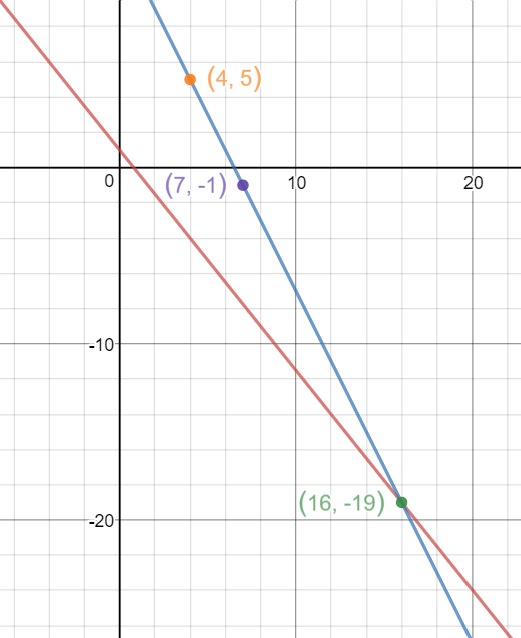Desmos.com

We're almost done. Our final steps are to find the length of #AB#, find the length of #BC#, and finally, to find #(AB)/(BC)#.

We can use the distance formula to calculate both of those distances, obtaining

#AB=sqrt((7-4)^2+(-1-5)^2)=sqrt(3^2+(-6)^2)=sqrt(9+36)#
#=sqrt9sqrt(1+4)=3sqrt5#

#BC=sqrt((16-7)^2+(-19-(-1))^2)=sqrt(9^2+(-18)^2)#
#=sqrt(9^2+9^2(-2)^2)=sqrt(9^2)sqrt(1+(-2)^2)=9sqrt(5)#

And a ratio between the two of:

#(AB)/(BC)=(3sqrt(5))/(9sqrt(5))=3/9=1/3#

Shiva Prakash M V
Feb 17, 2018

Hence, the ratio in which the point divides the line is
#4:-3=-4:3#

Explanation:

We need to find the point of intersection of the lines
#5x+4y=4# and
#(y-5)/(x-4)=(-1-y)/(7-x)#

Simplifying the second line

#(y-5)(7-x)=(-1-y)(x-4)#

#(y-5)(x-7)-(y+1)(x-4)=0#

Expanding
#xy-7y-5x+35-(xy-4y+x-4)=0#

#xy-7y-5x+35-xy+4y-x+4=0#

Rearanging and simplifying
#-6x-3y+39=0#
Dividing by 13
#-2x-y+13=0#

or

#2x+y=13#

The equations are:

#5x+4y=4#-------(1)
#2x+y=13#-------(2)

#detA=5xx1-2xx4=5-8=-3#
#detx=4xx1-13xx4=4-52=-48#
#dety=5xx13-2xx4=65-8=57#

#x=detx/detA=-48/-3=16#
#y=dety/detA=57/-3=-19#

#(x,y)-=(16,-19)#

Check

#5x+4y=5xx16+4xx(-19)=80-76=4#

#2x+y=2xx16+(-19)=32-19=23#

Verified.

Hence, the intersection point is #P-=(16,-19)#
One end of the line is
Other end of the line is #B-=(7,-1)#
Arranging in the form of #APB#
#(x_A,y_A)-=(4,5)#
#(x_P,y_P)-=(16,-19)#
#(x_B,y_B)-=(7,-1)#
P divides AB in the ratio
#(x_P-x_A)/(x_B-x_P)=(16-4)/(7-16)=12/-9=4/-3#along x axis
#(y_P-y_A)/(y_B-y_P)=(-19-5)/(-1-(-19))=(-24)/18=(-4)/3 #along y axis
Check:
Both are same
Justifying the coordinate for intersection point

Hence, the ratio in which the point divides the line is
#4:-3=-4:3#

Related questions
Impact of this question
4184 views around the world
You can reuse this answer
Creative Commons License