Find the ratio in which the staight line 5x+4y=4 divides the join of (4,5) and (7,-1)?
2 Answers
Explanation:
There are a few things we'll need to establish before we can find the requested ratio. If we want a ratio between two line segments, we'll obviously need two line segments, and in order to have two line segments, we'll need three points. Two points -
Before we can do that, though, we'll need to find the equation for
Here, we can take our two points to find that
With that in place, we can derive the general form of the line's equation by fixing one point in place - say,
Now that we have that equation, we can set up a system and solve for the intersection of the two:
Here, I'll solve by substition by first manipulating the second equation to get:
which, substituting into
Solving for
So our point of intersection is
For a feel as to what our picture looks like at this point:
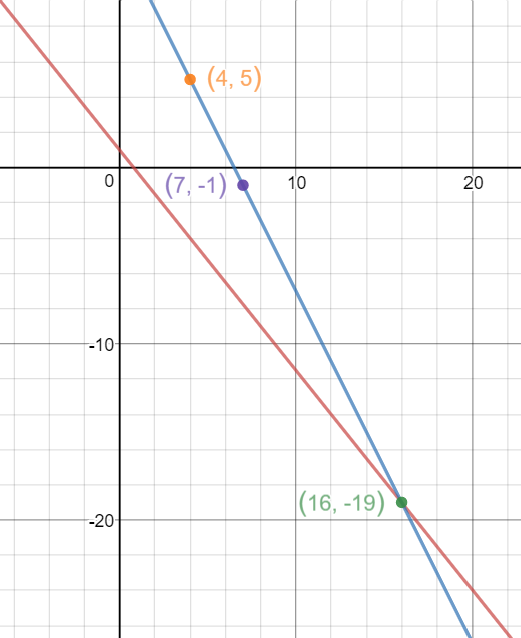 Desmos.com
Desmos.com
We're almost done. Our final steps are to find the length of
We can use the distance formula to calculate both of those distances, obtaining
And a ratio between the two of:
Hence, the ratio in which the point divides the line is
Explanation:
We need to find the point of intersection of the lines
Simplifying the second line
Expanding
Rearanging and simplifying
Dividing by 13
or
The equations are:
Check
Verified.
Hence, the intersection point is
One end of the line is
Other end of the line is
Arranging in the form of
P divides AB in the ratio
Check:
Both are same
Justifying the coordinate for intersection point
Hence, the ratio in which the point divides the line is


