Question

How do you graph `f(x)=2x+1` and then use the horizontal test to determine whether the inverse of f is a function?

Answer 1

Find your intercepts, connect and continue in each direction, draw a horizontal line through various points of the graph and make sure it never intersects more than once.

Explanation:

Find the x and y intercepts of `f(x)`:

y-intercept:

`f(0)=2(0)+1=1`

`(0,1)` is our y-intercept.

`2x+1=0`

`2x=-1` `x=-1/2`

`(-1/2,0)` is our x-intercept.

Plot these two points on the graph, connect them, and continue in each direction.

graph{2x+1 [-7.9, 7.9, -3.95, 3.95]}

For the inverse of f(x) to be a function, a horizontal line drawn through the graph of `f(x)` at any given point should intersect the graph no more than once.

Here, we can see that would certainly apply.

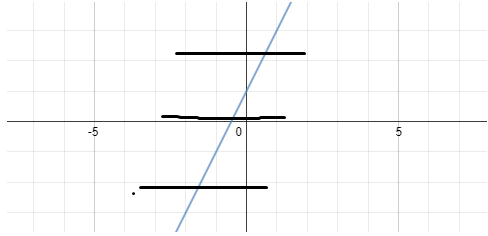
Thus, the inverse of `f(x)`, denoted by `f^(-1)(x)`, is a function.