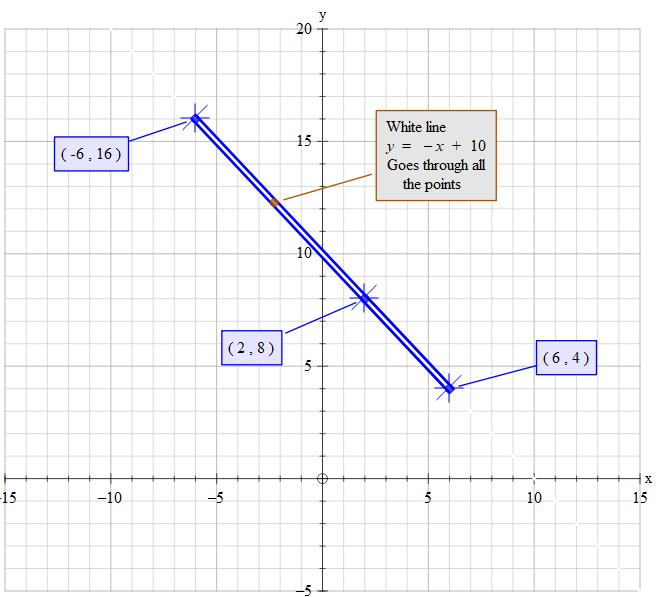
A(2,8), B(6,4) and C(-6,y) are collinear points find y?
3 Answers
Explanation:
If a set of points are collinear the belong to the same straight line, whose generale equation is
If we apply the equation to the point A we have:
If we apply the equation to the point B we have:
If we put this two equation in a system we can find the equation of the straight line:
- Find
mm in the first eq.
m=(8-q)/2m=8−q2 - Replace
mm in the second eq. and findqq
4=6(8-q)/2=>4=3(8-q)+q=>4=24-3q+q=>-20=-2q=>q=104=68−q2⇒4=3(8−q)+q⇒4=24−3q+q⇒−20=−2q⇒q=10 - Replace
qq in the first eq.
m=(8-10)/2=-1m=8−102=−1
Now we have the equation of the straight line:
y=-x+10y=−x+10
If we replace C coordinates in the equation we have:
y=6+10=>y=16y=6+10⇒y=16
Explanation:
Prerequisite :
Therefore, in our Problem,
Full details shown. With practice you will be able to do this calculation type with very few lines.
Explanation:
Lets split it into two parts
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The gradient for part is the same as the gradient for all of it
Gradient (slope)
Set point
Set point
Set point
The gradient ALWAYS reads left to right on the x-axis (for standard form)
So we read from
Set gradient
Negative 1 means that the slope (gradient) is downward as you read left to right. For 1 across there is 1 down.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Determined that
Multiply both sides by (-8)
Add 8 to both sides
 Tony B
Tony B

