Question

The equation of a line is `2x + 3y - 7 = 0`, find:- (1) slope of line (2) the equation of a line perpendicular to the given line and passing through the intersection of the line `x-y+2=0 and 3x + y-10=0`?

Answer 1

`-3x+2y-2=0 color(white)("ddd")->color(white)("ddd") y=3/2x+1`

First part in a lot of detail demonstrating how first principles work.
Once used to these and using shortcuts you will use a lot less lines.

Explanation:

`color(blue)("Determine the intercept of the initial equations")`

`x-y+2=0" ".......Equation(1)`
`3x+y-10=0" "....Equation(2)`

Subtract `x` from both sides of `Eqn(1)` giving

`-y+2=-x`
Multiply both sides by (-1)

`+y-2=+x" "..........Equation(1_a)`

Using `Eqn(1_a)` substitute for `x` in `Eqn(2)`

`color(green)(3color(red)(x)+y-10=0color(white)("ddd")->color(white)("ddd")3(color(red)(y-2)) +y-10=0`

`color(green)(color(white)("dddddddddddddddd")->color(white)("ddd")3y-6color(white)("d")+y-10=0)`

`color(green)(color(white)("dddddddddddddddd")->color(white)("ddddddd") 4y-16=0`

Add 16 to both sides

`color(green)(color(white)("dddddddddddddddd")->color(white)("ddddddd") 4y=16`

Divide both sides by 4
`color(green)(color(white)("dddddddddddddddd")->color(white)("ddddddd") y=4`

Substitute for `y` in `Eqn(1)` gives `color(green)(x=2)`

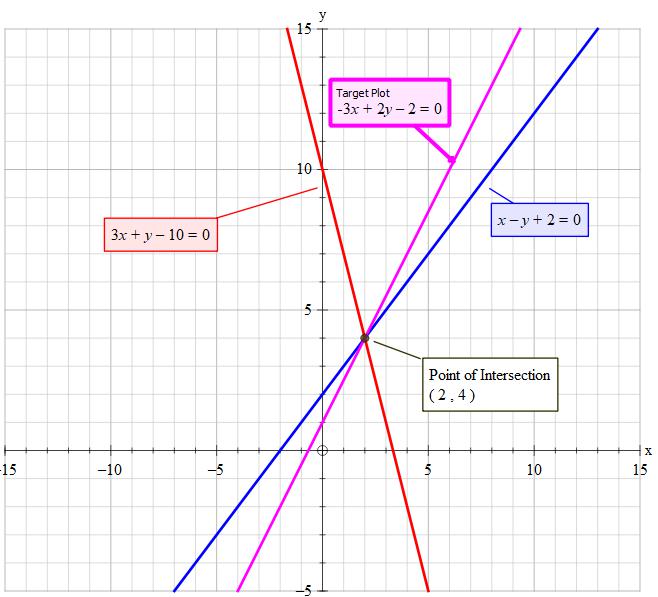
So the intersection of `Eqn(1) and Eqn(2) ->(x,y)=(2,4)`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`color(blue)("Determine the equation of the target plot")`

Given line: `2x+3y-7=0 color(white)("ddd")->color(white)("ddd")y=-2/3x+7/3`

Turn the `-2/3` upside down
Thus the gradient of the target line is `(-1)xx(-3/2)=+3/2`

Using `m=(y_2-y_1)/(x_2-x_1)color(white)("ddd")->color(white)("ddd")+3/2=(4-y_1)/(2-x_1)`

`3(2-x)=2(4-y)`

`6-3x=8-2y`

`-3x+2y-2=0 color(white)("ddd")->color(white)("ddd") y=3/2x+1`

Answer 2

Slope of the given line is `-2/3`
Equation of the perpendicular line is `y =3/2 x +1`

Explanation:

Equation of the line is `2x+3y-7=0 or 3y =-2x+7` or

`y =-2/3x+7/3 [y=mx+c] :. m= -2/3` . Slope of the line

is `-2/3` Let the coordinate of intersecting point of two lines

`x-y+2=0(1) and 3x+y-10=0(2)` be `(x_1,y_1)`

`:. x_1-y_1= -2(3) and 3x_1+y_ 1=10(4)` Adding

equation(3) and equation (4) we get , `4x_1=8` or

`x_1=2 : y_1=10 - 3x_1 or y_1= 10-3*2=4`. Therefore

intersecting point is `(2,4)` . Slope of the line perpendicular

to the line is `2x+3y-7=0` is `m_1= -1/m= 3/2` . Hence

equation of the perpendicular line in point slope form is

`y-y_1=m(x-x_1) or y-4= 3/2(x-2)` or

`y= 3/2x-3+4 or y =3/2 x +1` [Ans]