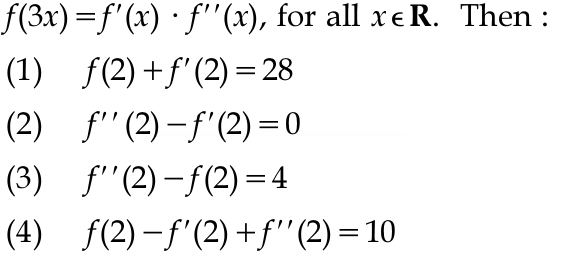If f(x) is of first degree its second derivative is identically null, so also f(x) would have to be identically null. to satisfy the equation f(3x) = f'(x)f''(x)
Let then f(x) be a generic polynomial of degree n >= 2. Then f'(x) will have degree (n-1) and f''(x) degree (n-2)
Now, the product f'(x)*f''(x) is a polynomial of degree (n-1)+(n-2) and as two polynomials can be equal for every x only if they have the same degree:
(2) " " f(3x) = f'(x)*f''(x)
implies:
n = (n-1)+(n-2)
n = 2n -3
n=3
that is f(x) must be of third degree:
f(x) =ax^3+bx^2+cx+d
f'(x) = 3ax^2+2bx+c
f''(x) = 6ax+2b
then (2) becomes:
27ax^3+9bx^2+3cx+d = (3ax^2+2bx+c)(6ax+2b)
27ax^3+9bx^2+3cx+d = 18a^2x^3+12abx^2+6acx+ 6abx^2+4b^2x+2bc
27ax^3+9bx^2+3cx+d = 18a^2x^3+18abx^2+(6ac+4b^2)x+ 2bc
Equating the coefficients of the same degree we get:
27a = 18a^2
and so as a!=0
a=3/2
Then:
9b = 18ab = 27b
b=0
at the first degree:
3c = 6ac+4b^2
3c = 9c
c = 0
and finally:
d= 2bc = 0
The polynomial which satisfies the equation is then:
f(x) = 3/2x^3
so that:
f'(x) = 9/2x^2
f''(x) = 9x
f(2) = 12
f'(2) = 18
f''(2) = 18
and only the second statement is correct.