Note that #2log_x(3)->log_x(3^2)=log_x(9)#
#log_3(x)-log_x(9)=1#
#log_3(x)=1+log_x(9)#
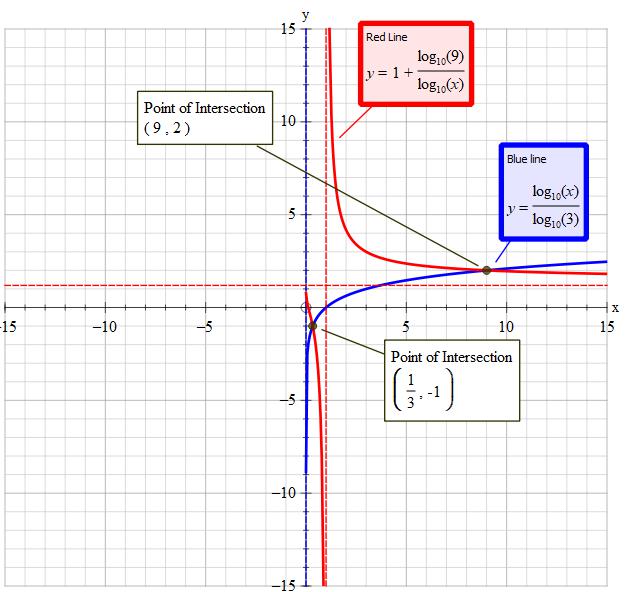
Consider the LHS #->log_10(x)/log_10(3) " "...Equation(1) =y_1#
Consider the RHS #->1+log_10(9)/(log_10(x))" "..Equation(2)=y_2#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
As we have got all #log_10# now we can drop the base 10 and use just log.
Try #y_1=y_2# and see what happens.
#log(x)/log(3)=1+log(9)/(log(x))#
#log(x) /log(3) = (log(x)+log(9))/log(x)#
Cross multiply
#log(x)^2=log(x)log(3)+log(3)log(9)#
Set #log(x) = t# giving
#t^2-tlog(3)-log(3)log(9)=0 larr" A quadratic in "t#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#y=ax^2+bx+c -> x=(-b+-sqrt(b^2-4ac))/(2a)#
Where #a=1; b=-log(3); c= -log(3)log(9)#
#t=(+log(3)+-sqrt(log(3)^2-4(1)(-log(3)log(9))))/(2(1))#
#t=+log(3)/2+-sqrt(2.0488022...)/2#
#t~~+0.95424...=>log^-1(t)= 9 = x#
#t~~-0.4771212....=>log^(-1)(t)= 1/3=x#