How do you verify the identify sintheta/csctheta=sin^2theta?
3 Answers
Explanation:
See Below.
Explanation:
 AllAboutCircuits
AllAboutCircuits
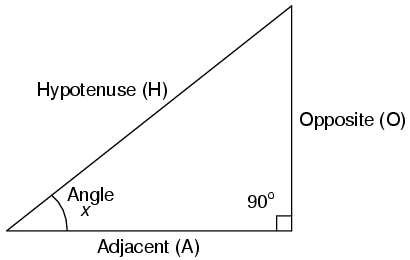
Trigonometric Ratios are of 6 kinds.
So, you can see that,
So,
L.H.S =
Hence Proved.
See Below.
 AllAboutCircuits
AllAboutCircuits
Trigonometric Ratios are of 6 kinds.
So, you can see that,
So,
L.H.S =
Hence Proved.