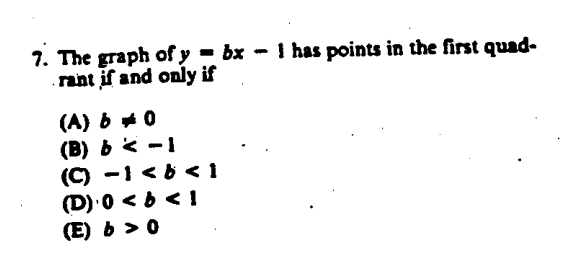In the general linear relation #y=bx+c#, the value of #b# controls the angle of the line, and the value of #c# controls the (vertical) shift.
If we fix #b# at something like #b=2# and let #c# change, the graph of #y=2x+c# will move up and down, but its slope stays the same.
Here, we see the graphs of #y=2x+3# and #y=2x-1:#
graph{(y-2x-3)(y-2x+1)=0 [-10, 10, -5, 5]}
If instead we fix #c# at something like #c=–1# and let #b# change, the graph of #y=bx-1# will rotate about the intercept #(0, –1).#
Here, we see the graphs of #y=2x-1# and #y=1/2x-1:#
graph{(y-2x+1)(y-x/2+1)=0 [-10, 10, -5, 5]}
If #b# is negative, the line will fall to the right, as in the graph of #y=–x-1# below:
graph{(y+x+1)=0 [-10, 10, -5, 5]}
As long as #b# is positive, the line will rise to the right, eventually making its way into the top-right quadrant, a.k.a. #Q_"I"#, the first quadrant, as in #y=1/10 x -1# below:
graph{(y-1/10x+1)=0 [-5, 15, -5, 5]}