How do you approach and solve this problem?
A curve called a witch of Maria Agnesi consists of all possible positions of the point P in the figure. Show that parametric equations for this curve can be written as
#x=2acottheta#
#y=2asin^2theta#
Sketch the curve.
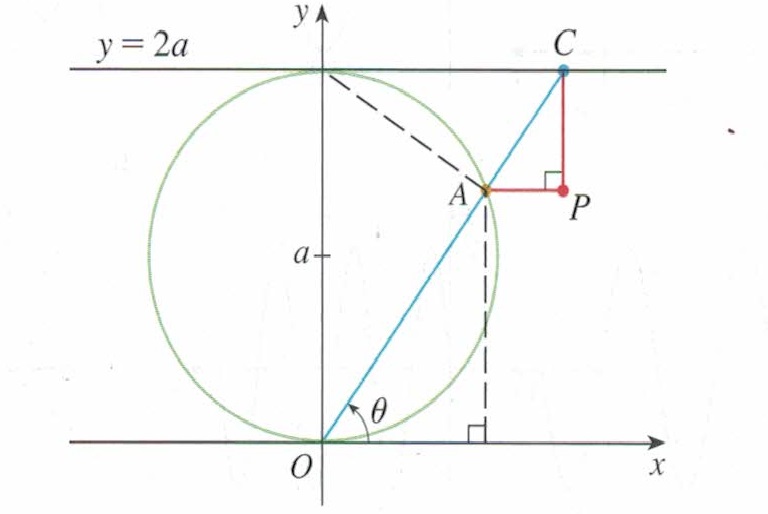
A curve called a witch of Maria Agnesi consists of all possible positions of the point P in the figure. Show that parametric equations for this curve can be written as
Sketch the curve.

1 Answer
Please see below.
Explanation:
As point
For this purpose and to explain it better, I intend to draw a perpendicular from
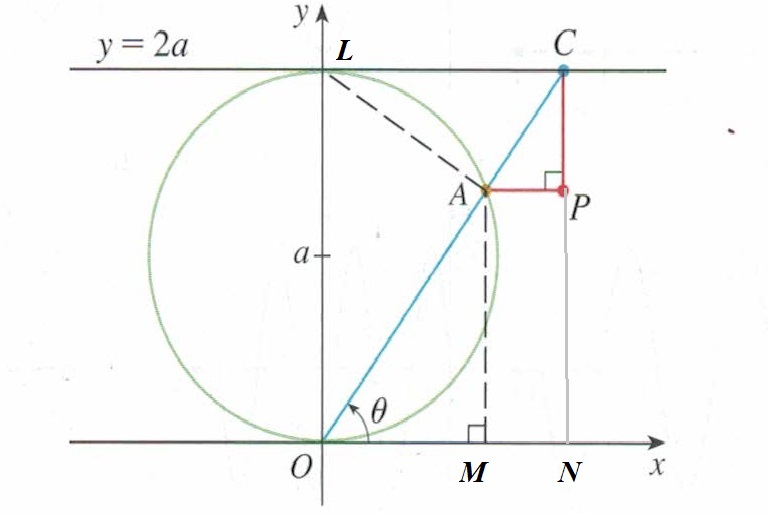
Now
and
but in
Therefore
Hence, parametric form of all possible positions of the point
We can also find locus in rectangular coordinates too by eliminating
Observe that
=
=
i.e.
and if
graph{(1000/y-100-x^2)(x^2+y^2-10y)=0 [-22.5, 22.5, -7.71, 14.79]}
