How do you find the exact value of the following using the unit circle 6 cos (11pi/6) - 2 sin^2 (5pi/4)?

Question

9711 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-03-17T05:44:37

#color(purple)(6 cos ((11pi)/6) - 2 sin ^2 ((5pi)/4) = 2#

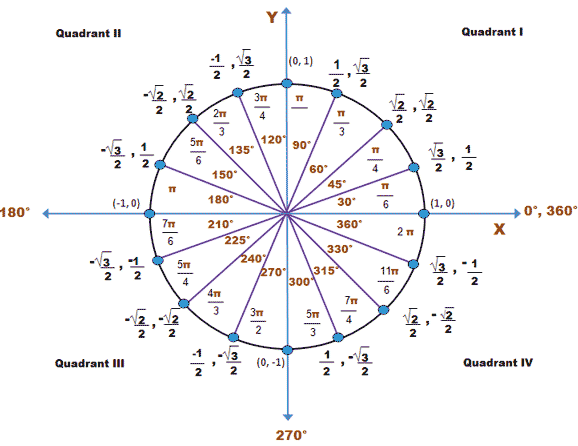
enter image source here

From the above diagram,

#hat (11pi)/6# is in IV quadrant where cos is positive.

#cos ((11pi)/6) = cos (((11pi)/6) - 2pi) = cos -(pi/6) = cos (pi/6)#

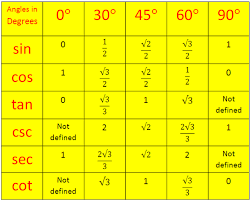
enter image source here

But #cos (pi/6) = cos 60 = x = 1/2# #:. color(red)(cos ((11pi)/6) = 1/2#

#hat (5pi)/4# is in III Quadrant where sin is negative.

#sin ((5pi)/4) = sin (pi + (pi/4)) = - sin (pi/4) = - sin 45#

But #sin (pi/4) = 1/sqrt2#

#:. color(green)(sin ((5pi)/4) = y = -1/sqrt2#

Returning to the given sum,

#6 cos ((11pi)/6) - 2 sin ^2 ((5pi)/4) = 6 * (1/2) - 2 (-(1/sqrt2))^2#

# => (6 * (1/2)) -(2* (1/2)) = 3 - 1 = 2#