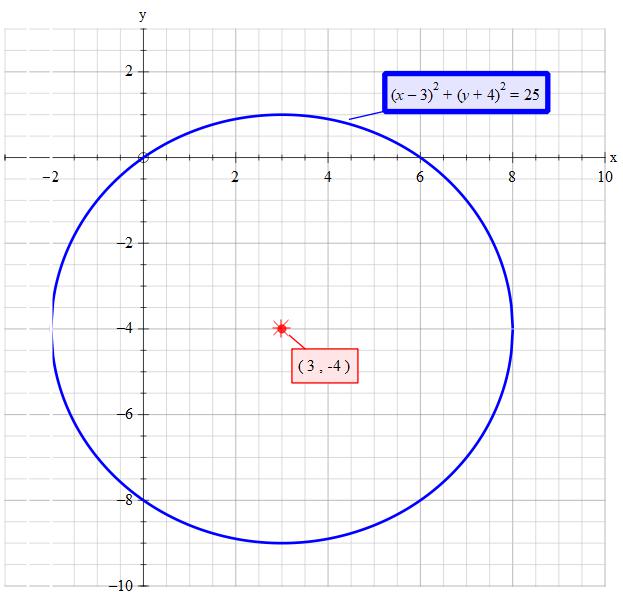
How do you find the center of the circle with equation #(x - 3)^ 2 + (y + 4)^ 2 = 25#?
2 Answers
Explanation:
the standard eqn of a circle with centre
is
so for
comparing this with
the centre will be
for good measure the radius will be
Centre
Explanation:
Note that the equation of a circle centred at the origin is derived using Pythagoras. This is because you can form a triangle related to any point on the perimeter.
The behaviour of the question's equation is such that it models the following:
Draw the circle at the origin where
Move every point that is at
Move every point that is at
The net effect is that you move the plot to the right by 3 and down by 4. This puts the new centre at
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Consider the
This is in fact:
So
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Consider the
This is in fact:
So
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~