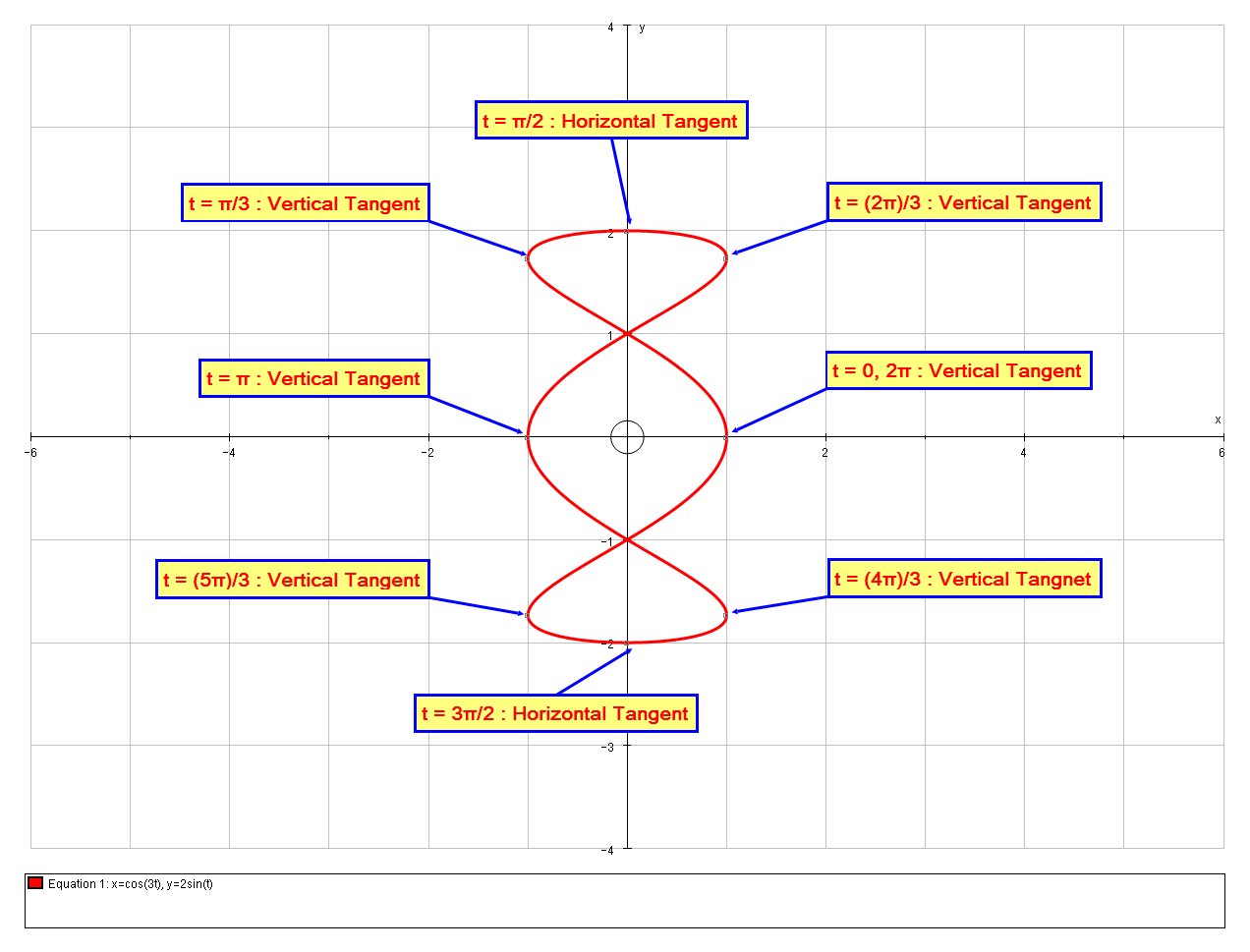
How do you find the horizontal and vertical tangents to #x = Cos(3t)# and #y = 2sin(t)#?
2 Answers
Recall that
#(dy/(dt))/(dx/(dt)) = dy/dx#
Therefore
#dy/dx = (2cost)/(-3sin(3t))#
Horizontal tangents occur when the derivative equals
#0 = 2cost -> t = pi/2 + pin#
Vertical tangents occur when the derivative is undefined.
#-3sin(3t) =0 -> 3t = pin -> t = pi/3n#
Hopefully this helps!
Horizontal Tangents occur when
Vertical Tangents occur when
Explanation:
We have the following parametric equation:
# x = cos(3t) # ... [A]
# y =2sin(t) # ... [B]
The entire curve is mapped out for
Horizontal tangents occurs when
# dy/dx = (dy//dt) /(dx//dt)#
Horizontal Tangents:
Differentiating [B] wrt
#t# we get:
# dy/dt = 2cost #
# dy/dt = 0 => 2cost = 0 #
# :. cost=0 => t = pi/2, (3pi)/2 \ " for " \ t in [0,2pi]#
Vertical Tangents:
Differentiating [A] wrt
#t# we get:
# dx/dt = -3sin(3t) #
# dx/dt = 0 => -3sin(3t) = 0 #
# :. sin(3t)=0 => 3t = 0, pi, 2pi, 3pi, 4pi, 5pi, 6pi \ " for " \ 3t in [0,6pi]#
# :. t = 0, pi/3, (2pi)/3, pi, (4pi)/3, (5pi)/3, 2pi \ " for " \ t in [0,2pi]#
The last value of