Question

Can somebody please explain to me the signs used for ∂m in this solution, with regard to the 'u'. I do not understand why '-|∂m|' is used, and then how it is later changed to a '+∂m'? Thanks in advance!

Answer 1

I agree. The use of `|deltam|` is unclear

Explanation:

I agree I think what the person who wrote the mark scheme is getting at, in a rather muddled notation, is that there are various ways of drawing the momentum diagram depending on whether you think of the system as starting with mass `m` or with mass `m+delta m` and how you label the exhaust.

They all boil down to the same final equation E1, They start off with different signs and arrow conventions, none of which include the `||` sign. In particular note that using the implications in the question `(dm)/(dt)` is negative and `u` and `v` are positive. For example, some people draw the "puff" of exhaust as having mass `-delta m`, leaving the end state of the rocket+fuel as mass `m+delta m`.

I assume you are happy with the dropping of the double increment `(delta m)(delta v)` when you "go to the limit" of the differential equation, either by maths or by imagining the rocket to be emitting regular "puffs" of exhaust of mass `delta m` (or `-delta m`) every `delta t`!)

Answer 2

Firstly the symbol that is used in the question is `delta` (Greek lower case delta) rather than `del`, the del symbol.

In this context `delta` is being used to denote a small increment. This is typically used in the standard notation for the limit definition of the derivative.

You may be familiar with the limit definition of the derivative:

`f'(x) = lim_(h rarr 0) ( f(x+h) - f(x) ) / h`

Using the delta notation we can write this as:

# f'(x) = lim_(deltax rarr 0) ( f(x+ deltax) - f(x) ) / (deltax) #

And, this is the meaning of the notation in the text.

As for the query, this is because because here `delta m` represent a small increment in mass. mass is (and must be) a positive quantity, however a body can lose or gain a small increment in mass during a "collision". In the case the rocket loses mass.

The way I would approach the problem is as follows:

If we consider a small time period `delta t` in which a small amount of matter (mass) `delta M` is ejected from the rocket of mass `M` at speed `u` causing an increase in velocity of the rocket of `deltav`.

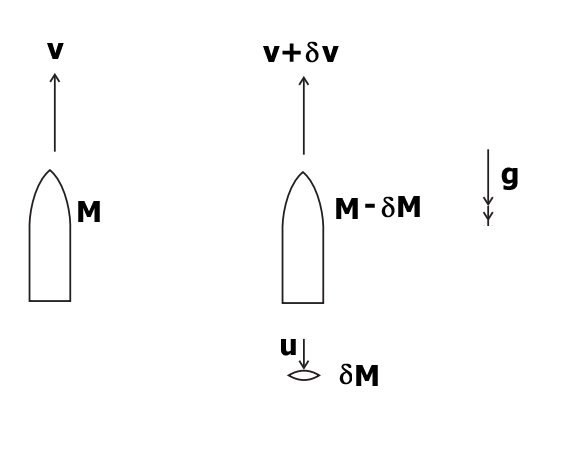
If the rocket has initial speed `v`(vertically upwards), and we consider the motion Vertically upwards then we can ignore vectors and calculate:

# {: ( "Initial Momentum", = Mv), ( "Final Momentum", = (M-deltaM)(v+deltav) + (deltaM)(v-u)) :} #

Using:

Impulse = changes momentum we get (as indicated):

We have:

`-Mg(deltat) = {(M-deltaM)(v+deltav) + (deltaM)(v-u)} -Mv`

`:. Mv+Mdeltav-deltaMv-deltaMdeltav+ deltaMv-deltaM u -Mv = -Mgdeltat`

`:. Mdeltav-deltaMdeltav-udeltaM = -Mgdeltat`

`:. M(deltav)/(deltat)-deltaM(deltav)/(deltat)-u(deltaM)/(deltat) = -Mg`

The we take the limit as `delta t rarr 0 => delta M rarr 0` giving us :

`lim_(delta t rarr 0) {M(deltav)/(deltat)-deltaM(deltav)/(deltat)-u(deltaM)/(deltat)}= -Mg`

And using the limit definition of the derivative, this becomes:

`M(dv)/(dt)-0-u(dM)/(dt) = -Mg`

`:. M(dv)/(dt)-u(dM)/(dt) = -Mg`

And we note that `(dm)/dt` is the rate of increase of mass wrt time; thus:

`(dm)/dt = -(dM)/dt`

Giving us:

`m(dv)/(dt)+u(dm)/(dt) = -mg \ \ \ \` QED

Answer 3

Consider a rocket instantaneously emitting a "puff" of exhaust of mass `-δm` every `δt` seconds.

Taking vertically upward as positive velocity (and hence momentum), and using a frame of reference which is moving up at constant velocity `v` at some time `t`.

Take the "system" at time `t` (for the purpose of Newton's Laws) as being everything that has not been expelled from the exhaust (i.e. the system is the rocket casing plus the unused fuel at time `t`).

Then the momentum `M1` before the puff is zero.
The momentum `M2` just before the next puff is `(m+δm)δv -u(-δm)`.
The impulse `I` during the interval `δt` is `-mgδt` (i.e. weight times time).
Now `M2-M1=I` (Conservation of linear momentum, or "impulse = change in momentum", whatever you like).

So
`(m+δm)δv+uδm - 0=-mgδt`

`mδv+δmδv+uδm=-mgδt`

`mδv+uδm+δmδv=-mgδt`

`m(δv)/(δt)+u(δm)/(δt)+(δmδv)/(δt)=-mg`

In the limit as `δt to 0`, the differential `(δmδv)/(δt)` dissappears and you get
`m(dv)/(dt)+u(dm)/(dt)=-mg`

Final observations:
1. Taking the frame of reference to a CONSTANT VELOCITY frame which is moving at some instant at the same velocity as some (possibly accelerating or deforming) system is often very convenient for manipulating the algebra. Alternatively, you could have taken whatever frame of reference the `v` was using in the question. This would introduce a `v` into the equations which would clutter them up and before disappearing in a puff of smoke.

1. If you don't like the "negative" sign in the puff, you can use a positive sign, but in the last step you need to realise that `lim (δm)/(δt)=-(dm)/(dt)`, because by definition `(dm)/(dt)` is the rate of INCREASE of mass whereas `(δm)/(δt)` would be the rate of DECREASE of mass.

2. It is very important to apply conservation of momentum to a thermodynamic SYSTEM which you need to be clear in your mind. By definition, this is a defined set of particles which can change configuration. In this case, the system is (instantaneously) made up of two components: the mass of the structure of the rocket plus fuel NOT burnt during the interval `δt` , and the mass of fuel burnt during that interval. The first acquires the new velocity `δv`, the second acquires a velocity `-u`.