Can somebody please explain to me the signs used for ∂m in this solution, with regard to the 'u'. I do not understand why '-|∂m|' is used, and then how it is later changed to a '+∂m'? Thanks in advance!

3 Answers
I agree. The use of
Explanation:
I agree I think what the person who wrote the mark scheme is getting at, in a rather muddled notation, is that there are various ways of drawing the momentum diagram depending on whether you think of the system as starting with mass
They all boil down to the same final equation E1, They start off with different signs and arrow conventions, none of which include the
I assume you are happy with the dropping of the double increment
Firstly the symbol that is used in the question is
In this context
You may be familiar with the limit definition of the derivative:
# f'(x) = lim_(h rarr 0) ( f(x+h) - f(x) ) / h #
Using the delta notation we can write this as:
# f'(x) = lim_(deltax rarr 0) ( f(x+ deltax) - f(x) ) / (deltax) #
And, this is the meaning of the notation in the text.
As for the query, this is because because here
The way I would approach the problem is as follows:
If we consider a small time period
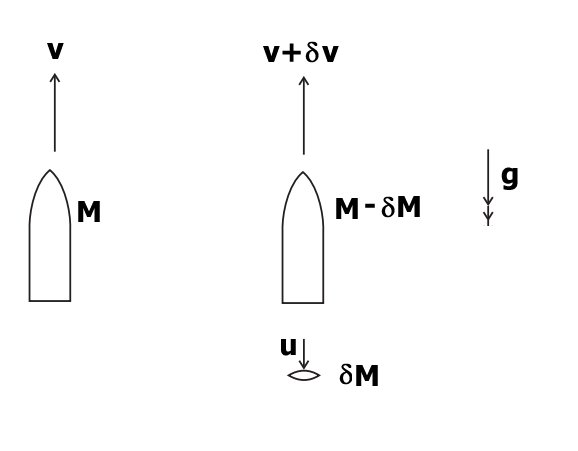
If the rocket has initial speed
# {: ( "Initial Momentum", = Mv), ( "Final Momentum", = (M-deltaM)(v+deltav) + (deltaM)(v-u)) :} #
Using:
Impulse = changes momentum we get (as indicated):
We have:
# -Mg(deltat) = {(M-deltaM)(v+deltav) + (deltaM)(v-u)} -Mv #
# :. Mv+Mdeltav-deltaMv-deltaMdeltav+ deltaMv-deltaM u -Mv = -Mgdeltat #
# :. Mdeltav-deltaMdeltav-udeltaM = -Mgdeltat #
# :. M(deltav)/(deltat)-deltaM(deltav)/(deltat)-u(deltaM)/(deltat) = -Mg #
The we take the limit as
# lim_(delta t rarr 0) {M(deltav)/(deltat)-deltaM(deltav)/(deltat)-u(deltaM)/(deltat)}= -Mg #
And using the limit definition of the derivative, this becomes:
# M(dv)/(dt)-0-u(dM)/(dt) = -Mg #
# :. M(dv)/(dt)-u(dM)/(dt) = -Mg #
And we note that
# (dm)/dt = -(dM)/dt #
Giving us:
# m(dv)/(dt)+u(dm)/(dt) = -mg \ \ \ \ # QED
Consider a rocket instantaneously emitting a "puff" of exhaust of mass
Taking vertically upward as positive velocity (and hence momentum), and using a frame of reference which is moving up at constant velocity
Take the "system" at time
Then the momentum
The momentum
The impulse
Now
So
In the limit as
Final observations:
1. Taking the frame of reference to a CONSTANT VELOCITY frame which is moving at some instant at the same velocity as some (possibly accelerating or deforming) system is often very convenient for manipulating the algebra. Alternatively, you could have taken whatever frame of reference the
-
If you don't like the "negative" sign in the puff, you can use a positive sign, but in the last step you need to realise that
#lim (δm)/(δt)=-(dm)/(dt)# , because by definition#(dm)/(dt)# is the rate of INCREASE of mass whereas#(δm)/(δt)# would be the rate of DECREASE of mass. -
It is very important to apply conservation of momentum to a thermodynamic SYSTEM which you need to be clear in your mind. By definition, this is a defined set of particles which can change configuration. In this case, the system is (instantaneously) made up of two components: the mass of the structure of the rocket plus fuel NOT burnt during the interval
#δt# , and the mass of fuel burnt during that interval. The first acquires the new velocity#δv# , the second acquires a velocity#-u# .

