How to calculate the derivative?
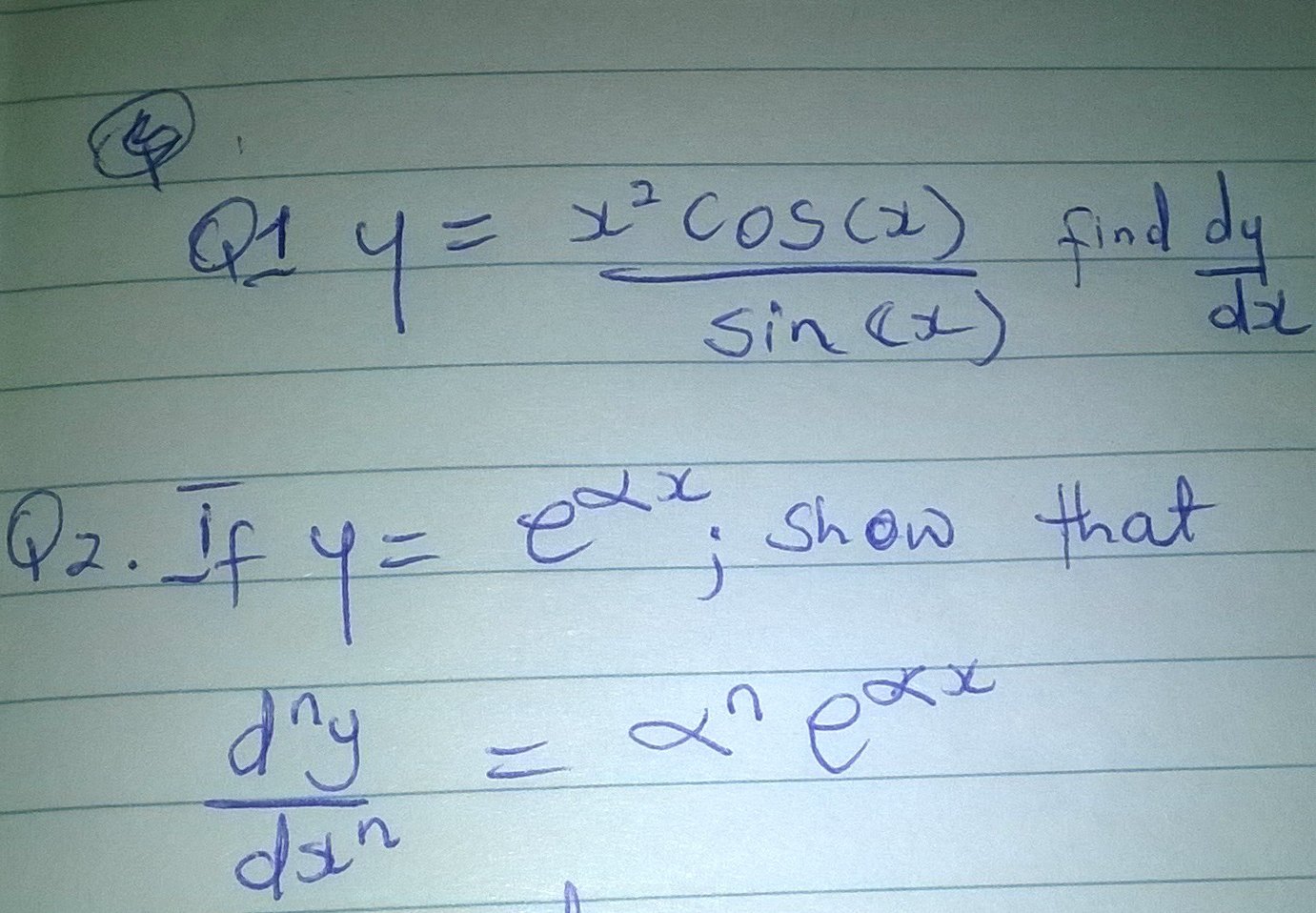
(Q1) If y = (x^2cos(x))/(sin(x)) , find (dy)/(dx) .
(Q2) If y = e^(alpha x) , show (d^ny)/(dx^n) = alpha^(n)e^(alpha x)
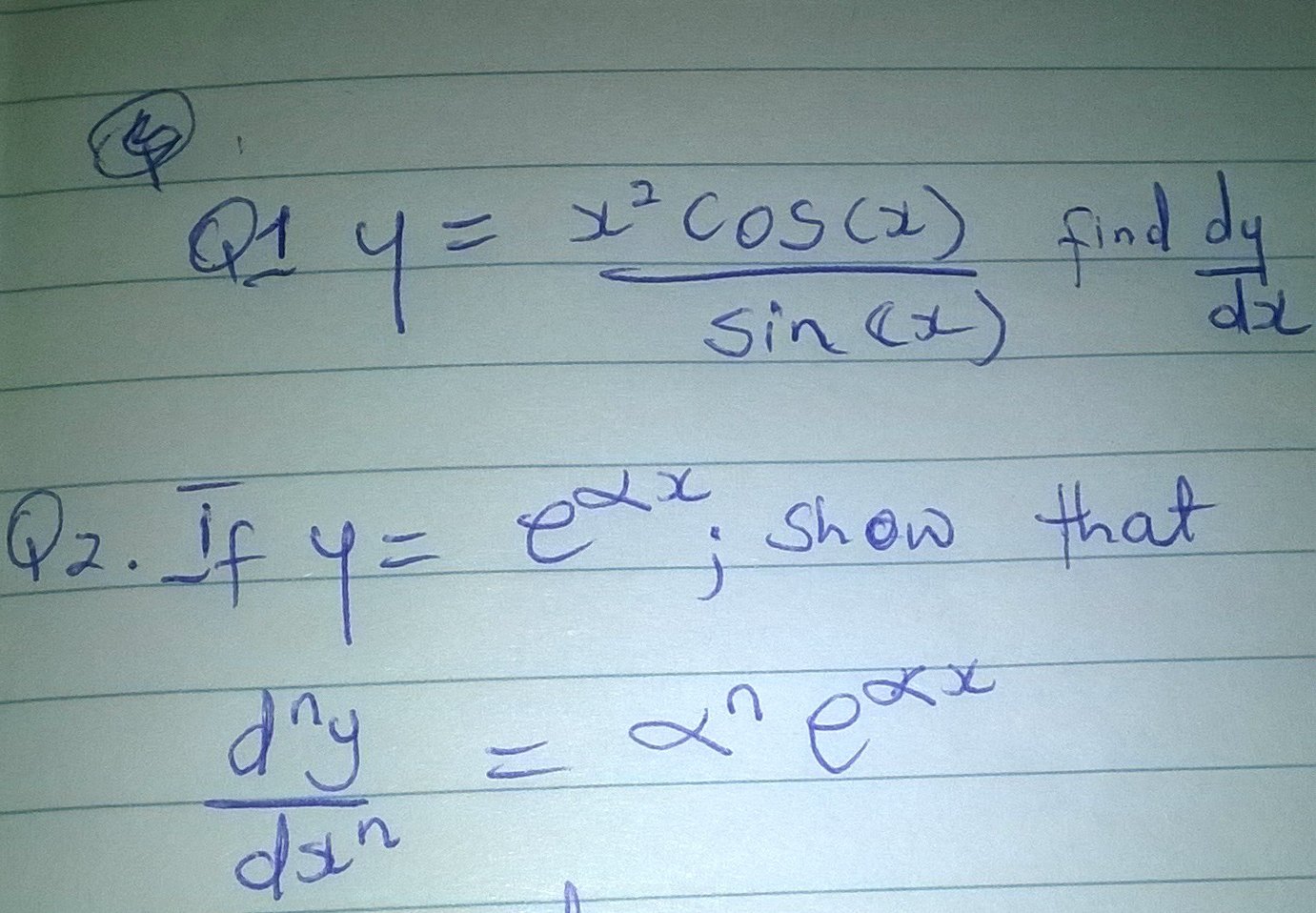
5 Answers
Q1:
Q2: See explanation below
Explanation:
Question 1:
We can simplify the expression using the trigonometric identity
Now simply apply the product rule.
Question 2:
Here's question
Let's create a table with the first few derivatives of
y' = alphae^(alphax)
y'' = alpha^2e^(alphax)
y''' = alpha^3e^(alphax)
(d^n y)/(dx^n) = alpha^n e^(alpha x)
As required.
Hopefully this helps!
Q1:
Explanation:
Q1 requires application of both the product rule and quotient rule.
Recall that if
For
Differentiate each of the above to have them on hand when applying the quotient rule.
So, using the above formula for the quotient rule,
Simplify:
For Q2, simply calculate the first few derivatives to recognize the pattern:
Applying the chain rule to differentiation:
So, the pattern is
Explanation:
=============EDIT=============
For math formatting, see this
A more rigorous proof for
Induction Proof - Hypothesis
We seek to prove that:
(d^(n))/(dx^n) e^(alpha x)= alpha^n e^(alpha x) ..... [A]
So let us test this assertion using Mathematical Induction:
Induction Proof - Base case:
We will show that the given result, [A], holds for
When
d/dx e^(alphax) = e^(alphax) d/dx (alphax)
\ \ \ \ \ \ \ \ \ \ = e^(alphax) d(alpha)
Or more precisely:
(d^(1))/(dx^1) e^(alphax) = d/dx = e^(alphax) = alpha^1e^(alphax)
So the given result is true when
Induction Proof - General Case
Now, Let us assume that the given result [A] is true when
(d^(m))/(dx^m) e^(alpha x)= alpha^m e^(alpha x) ..... [B]
We can now differentiate [B] a further time, and again apply the chain rule, to get:
d/dx ((d^(m))/(dx^m) e^(alpha x) ) = d/dx alpha^m e^(alpha x)
" " = alpha^m d/dx e^(alpha x)
" " = alpha^m \ e^(alpha x) \ d/dx (alpha x)
" " = alpha^m \ e^(alpha x) \ (alpha)
" " = alpha^(m+1) \ e^(alpha x)
Which is the given result [A] with
Induction Proof - Summary
So, we have shown that if the given result [A] is true for
(d^(m))/(dx^m) e^(alpha x) = alpha^m e^(alpha x) => (d^(m+1))/(dx^(m+1)) e^(alpha x) = alpha^(m+1) e^(alpha x)
where
(d^(1))/(dx^1) e^(alpha x) = alpha^1 e^(alpha x)
so it must also be true for
Induction Proof - Conclusion
Then, by the process of mathematical induction the given result [A] is true for
Hence we have:
(d^(n))/(dx^n) e^(alpha x)= alpha^n e^(alpha x) \ \ \ QED





