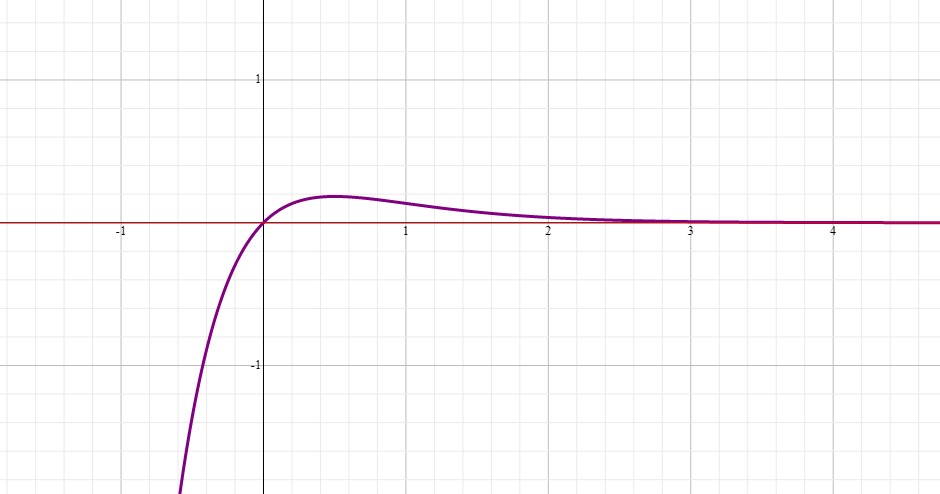
.
.
#y=xe^(-2x)#
Let's take the derivative of the function using the Product Rule:
#dy/dx=-2xe^(-2x)+e^(-2x)#
We set this derivative equal to #0# and solve for #x#:
#-2xe^(-2x)+e^(-2x)=0#
#e^(-2x)(-2x+1)=0#
#e^(-2x)=0, :. 1/e^(2x)=0, :. e^(2x)=oo, :. x=oo#
#-2x+1=0, :. 2x=1, :. x=1/2#
#x=oo# is not a maximum for the function.
#x=1/2# can be either a maximum or a minimum.
Let's find the #y# coordinate for this point:
#y=xe^(-2x)=1/2e^(-2(1/2))=1/2e^(-1)=1/2*1/e=1/(2e)#
The point has the coordinates of #(1/2,1/(2e))# or #(0.5,0.18)#
To find out whether the function is increasing or decreasing before and after this point, we use the derivative. We know that the slope of the tangent line to any curve at a specific point can be found by plugging the #x# coordinate of the point into the derivative function.
If the result is positive the tangent line has a positive slope #(m)# which means the function is increasing at that point (on the rise). If it is negative the function is decreasing at that point.
Let's test a point with the #x#-coordinate of #1/4# which is smaller than #1/2#:
#dy/dx=m=e^(-2x)(-2x+1)=e^(-2(1/4))(-2(1/4)+1)=e^(-1/2)(-1/2+1)=1/e^(1/2)*1/2=0.607*0.5=0.3035# a positive value
Now, let's try a point with the #x#-coordinate of #1# which is larger than #1/2#:
#dy/dx=m=e^(-2(1))(-2(1)+1)=e^(-2)(-1)=-1/e^2=-0.1353# a negative value
This indicates that the point #(0.5,0.18)# is a maximum because the function is increasing before it and decreasing after it.
And because we only have this one critical point, we can determine that the function is increasing when:
#-oo < x < 0.5#
And it is decreasing when:
#0.5 < x < oo#
Let's take the second derivative of the function:
#(d^2y)/(dx^2)=-2(-2xe^(-2x)+e^(-2x))-2e^(-2x)=4xe^(-2x)-2e^(-2x)-2e^(-2x)=4xe^(-2x)-4e^(-2x)#
#(d^2y)/(dx^2)=4e^(-2x)(x-1)#
We set this second derivative equal to #0# and solve for #x# to find the inflection point:
#4e^(-2x)(x-1)=0#
#e^(-2x)=0, :. 1/e^(2x)=0, :. e^(2x)=oo, :. x=oo# this is not a valid inflection point.
#x-1=0, :. x=1#
Let's plug this into the function to find its #y#:
#y=xe^(-2x)=(1)e^((-2)(1))=e^(-2)=1/e^2=0.13#
#(1,0.13)# is the inflection point.
Now, we can perform the second derivative test to determine concavity. We will test an #x# value smaller and one larger than #1#:
#x=0.9, :. (d^2y)/(dx^2)=4e^(-1.8)(0.9-1)=-0.066#
#x=1.1, :. (d^2y)/(dx^2)=4e^(-2.2)(1.1-1)=0.044#
This means the curve is concave up when:
#-oo < x < 1#
And it is concave down when:
#1 < x < oo#
There is no relative minimum or relative maximum. The maximum point we found is the absolute maximum. There is no absolute minimum either.
We set #x=0# to find the #y#-intercept:
#x=0, :. y=xe^(-2x)=0#
#(0,0)# is the #y#-intercept:
We set #y=0# to find the #x#-intercept:
#y=0, :. x=0, and e^(-2x)=0, :. 1/e^(2x)=0, :. e^(2x)=oo, :. x=oo#
#(0,0)# is the #x#-intercept.
#x=oo# when #y=0# indicates that the #x#-axis is the horizontal asymptote of the function.
#Lim_(x->+oo)xe^(-2x)=Lim_(x->+oo)x*1/e^(2x)=oo*1/oo=oo*0=0#
#Lim_(x->-oo)xe^(-2x)=-oo*+oo=-oo#
The graph of the function is: