Question

How do you simplify `-5(x-7)`?

Answer 1

`-5x + 35`

Explanation:

The easiest way to solve this problem is to use the distributive property:

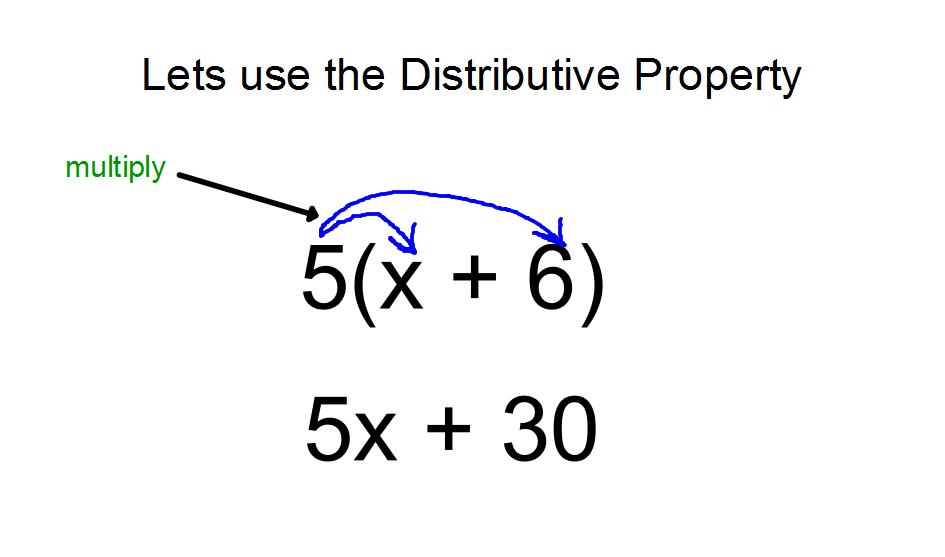https://sites.google.com/a/d83.org/math-6/chapter-6/6-6-the-distributive-property

Basically you multiply the number outside the parentheses by everything inside the parentheses.

`color(blue)(-5)(color(orange)x color(green)(- 7))`

`(color(blue)(-5) xx color(orange)x)` `+ (color(blue)(-5) xx color(green)(-7))`

`-5x + (+35)`

`color(white)"xxxxxxxxx"` `uarr` remember that #"negative" xx "negative" = "positive"#. That's why `35` is positive.

`-5x + 35`