Question

What are the intercepts of `3x - 5y^2 = 6`?

Answer 1

**`x` intercept: `(2, 0)`

`y` intercept: NONE**

Explanation:

Before we find the x intercept, let's first make `x` by itself:
`3x - 5y^2 = 6`

Add `5y^2` to both sides of the equation:
`3x = 6 + 5y^2`

Divide both sides by `3`:
`x = (6+5y^2)/3`

`x = 2 + (5y^2)/3`

To find the `x` intercept, we plug in `0` for `y`, and solve for `x`:
`x = 2 + (5(0)^2)/3`

`x = 2 + 0/3`

`x = 2 + 0`

`x = 2`

So we know that the `x` intercept is `(2, 0)`.

---

Now let's make `y` by itself to find the `y` intercept:
`3x - 5y^2 = 6`

Subtract `3x` from both sides of the equation:
`-5y^2 = 6 - 3x`

Divide both sides by `-5`:
`y^2 = (6-3x)/-5`

Square root both sides:
`y = +-sqrt((6-3x)/-5)`

Now plug in `0` for `x`:
`y = +-sqrt((6-3(0))/-5`

`y = +-sqrt(-6/5)`

Since you can't square root a negative number, that means the solution is imaginary, meaning that there is no `y` intercept.

To check that our intercepts are correct, we can graph this: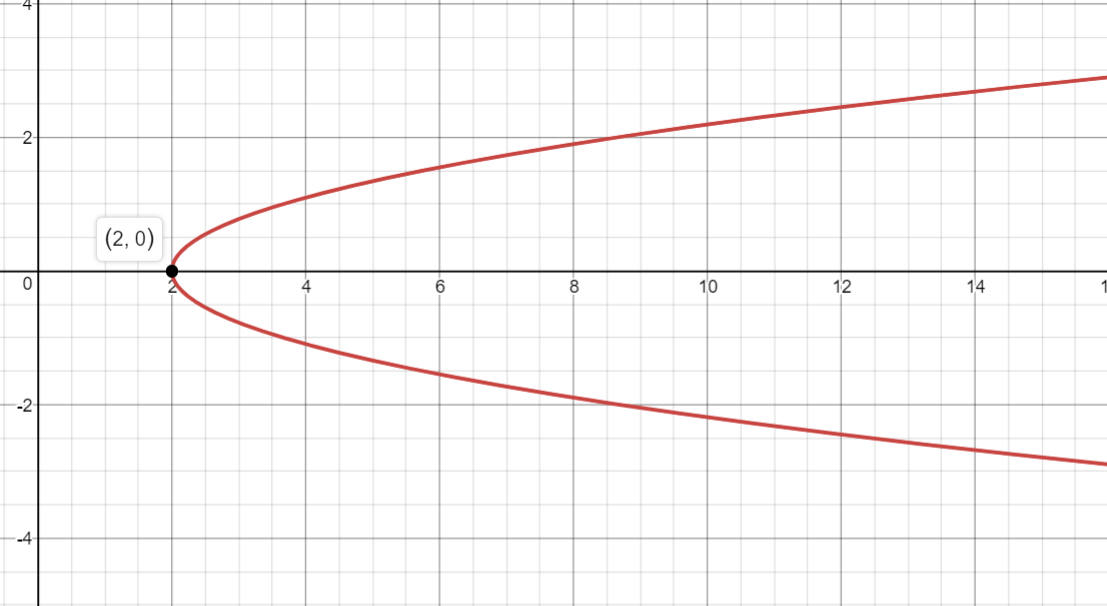

As you can see from the graph, it never touches the `y` axis, meaning that there is no value of `y` when `x` is zero. Also, you can see that the `x` intersect is in fact `(2, 0)`.

Hope this helps!