Question

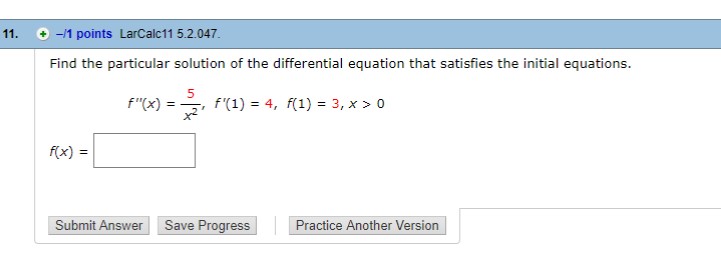
Find the particular solution of the differential equation that satisfies the initial equations?

Answer 1

The function is `f(x) =9x - 5lnx - 6`

Explanation:

Integrate to get the first derivative.

`f'(x) = -5/x + C`

From our conditions

`4 = -5/1 + C`

`C = 4 + 5 = 9`

Thus

`f'(x) =-5/x + 9`

Now integrate again to get `f(x)`.

`f(x) = -5ln|x| + 9x + C`

Once again solving for `C`:

`3= -5ln|1| + 9(1) + C`

`3 = 9 +C`

`C =-6`

Since `x> 0`, we can forget about the absolute value bars.

Hopefully this helps!