How do I find the angle between the line and its reflection in a plane?

Question

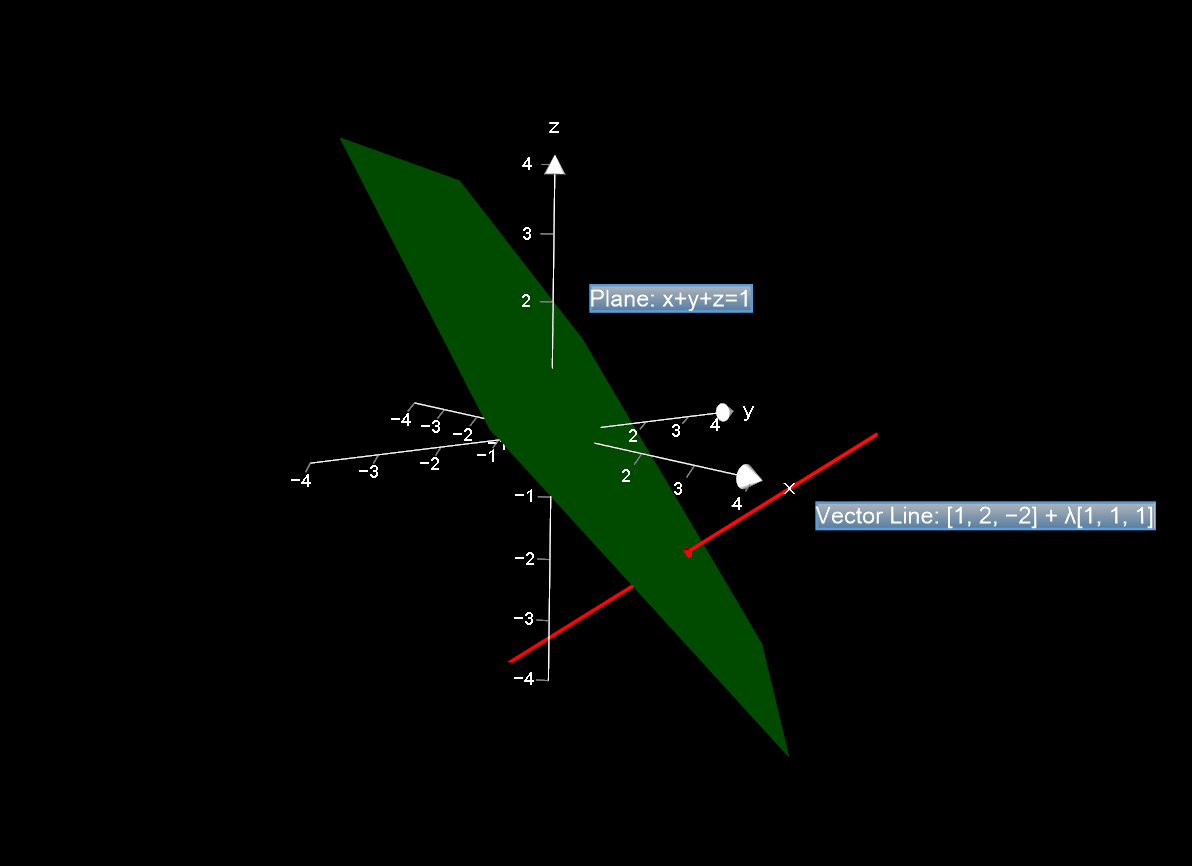
The line l: x= 1 + t, y= 2 + t, z= -2 + t , is reflected in the plane x+y+z=1. Calculate the angle between the line and its reflection.

1300 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-19T10:53:03

#color(blue)(90^@)#

First calculate 2 points in the plane #x+y+z=1#.

#P_1#:

#2+3+z=1=>z=-4#

#P_1=((2),(3),(-4))#

#P_2#

#1+2+z=1=>z=-2#

#P_2=((1),(2),(-2))#

Form a vector #V#

#vec(V)=P_2-P_1=((1),(2),(-2))-((2),(3),(-4))=((-1),(-1),(2))#

Convert parametric equation of the line into a vector equation of a line,

#x=1+t,y=2+t,z=-2+t#

#((1),(2),(-2))+lambda((1),(1),(1))#

All we need to do now is find the angle between:

#((1),(1),(1)) and ((-1),(-1),(2))#

Let #vec(W)=((1),(1),(1))#

#vec(V)* vec(W)=||V|| * ||W||* cos(theta)#

#vec(V)* vec(W)=1*(-1)+1*(-1)+1*(2)=0#

We don't need to go any further. This shows:

#cos(theta)=0=>theta=90^@#. The line is perpendicular to the plane.

This can be seen in the plot:

enter image source here

Answer 2 · 2018-04-19T11:24:32

#0 or pi#.

Observe that, the direction of the line, say #L#, is #vec l=(1,1,1)#.

Normal of the plane, say #Pi#, is #vec n=(1,1,1)#.

#vecl=vecn rArr L bot Pi#.

So, if #L'# is the line reflected in #Pi," then "L=L'#.

Hence, #/_(L,L')=0, or, pi#.