The Dot Product
Key Questions
-
That's very simple, I'll show you how,
Let,
A + B = CThus, one may write,
C. C = (A + B).(A + B)
this implies, that
#C^2 = A^2 + B^2 + 2AB Cos theta# Thus we get,
#C = [A^2 + B^2 +2AB Cos theta]^(1/2)# This, is the law of cosines.
-
The dot product of two vectors is a quite interesting operation because it gives, as a result, a...SCALAR (a number without vectorial properties)!
As a definition you have:
Given two vectors
#vecv# and#vecw# the dot product is given by:#vecv*vecw=|vecv|*|vecw|*cos(theta)# i.e. is equal to the product of the modules of the two vectors times de cosine of the angle between them.
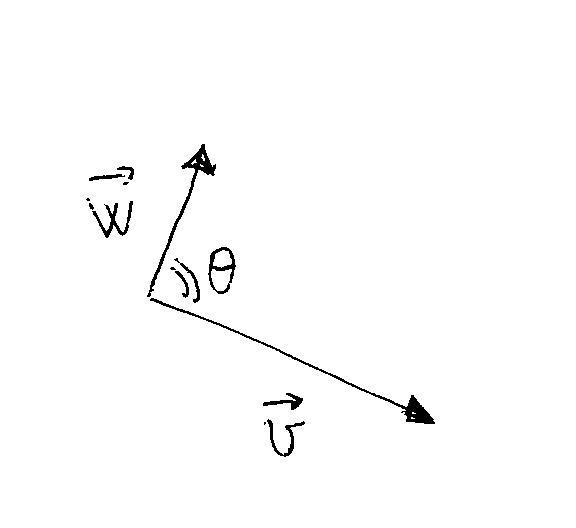
For example:
if#|vecv|=10# and#|vecw|=5# and#theta =60°#
#vecv*vecw=|vecv|*|vecw|*cos(theta)=10*5*cos(60°)=25# Another way of calculating the dot product is to use the coordinates of the vectors:
If you have:
#vecv=aveci+bvecj+cveck# and#vecw=dveci+evecj+fveck#
(where#a,b,c,d,e and f# are real numbers)
you can write:
#vecv*vecw=(a*d)+(b*e)+(c*f)#
For example:
if:
#vecv=3veci+5vecj-3veck# and#vecw=-1veci+2vecj+3veck#
#vecv*vecw=(3*-1)+(5*2)+(-3*3)=#
#=-3+10-9=-2# This operation has important practical applications. For example in Physics the dot product of Force (a vector) and displacement (a vector) gives as a result a number without vectorial characteristics, called, Work.
-
The cross product is used primarily for 3D vectors. It is used to compute the normal (orthogonal) between the 2 vectors if you are using the right-hand coordinate system; if you have a left-hand coordinate system, the normal will be pointing the opposite direction. Unlike the dot product which produces a scalar; the cross product gives a vector.
The cross product is not commutative, so
#vec u xx vec v!=vec v xx vec u# . If we are given 2 vectors:#vec u={u_1, u_2, u_3}# and#vec v={v_1, v_2, v_3}# , then the formula is:#vec u xx vec v={u_2*v_3-u_3*v_2, u_3*v_1-u_1*v_3, u_1*v_2-u_2*v_1}# 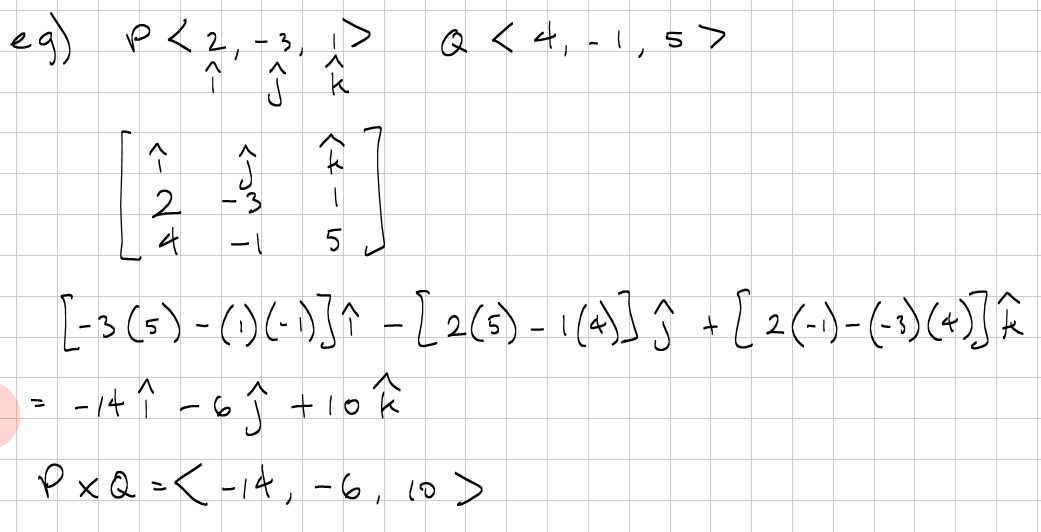
If you have learnt calculating determinants, you will notice that the formula looks a lot like cofactor expansion of the first row; only you don't add up the terms, the terms become the components of the normal. This is one way to remember how to generate the formula for cross product. This is why the middle component is negated in the example.