Question

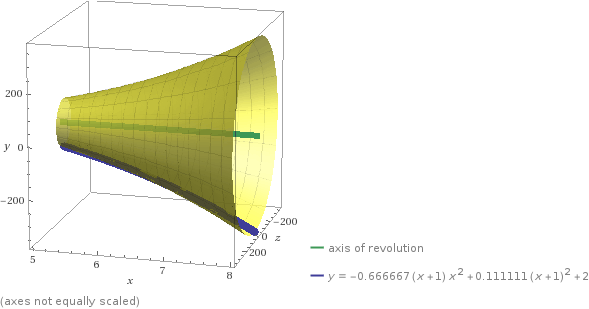
What is the surface area of the solid created by revolving `f(t) = ( 3t-1, t^2-2t+2), t in [2,3]` around the x-axis?

Answer 1

`=489392.457` Cubic units#

Explanation:

Parametric Equations

`x=3t-1`

`thereforet=(x+1)/3` `color(green)(rarr(1)`

`y=t^2-2t+2`

Substitute in `y`

`y=(x+1)^2/9-2xx(x+1)/3+2`

When

`tin[2,3]` `rarr` `x in[5,8]` `color(blue) (" from "` `color(green)((1)`

Determining the Volume of a Solid of Revolution

`V=piint_5^8((x+1)^2/9-2xx(x+1)/3+2)^2`

For this Integration, You will use `color(blue)("The Binomial Theorem and The Power Rule"`

`=489392.457` Cubic units#