Question

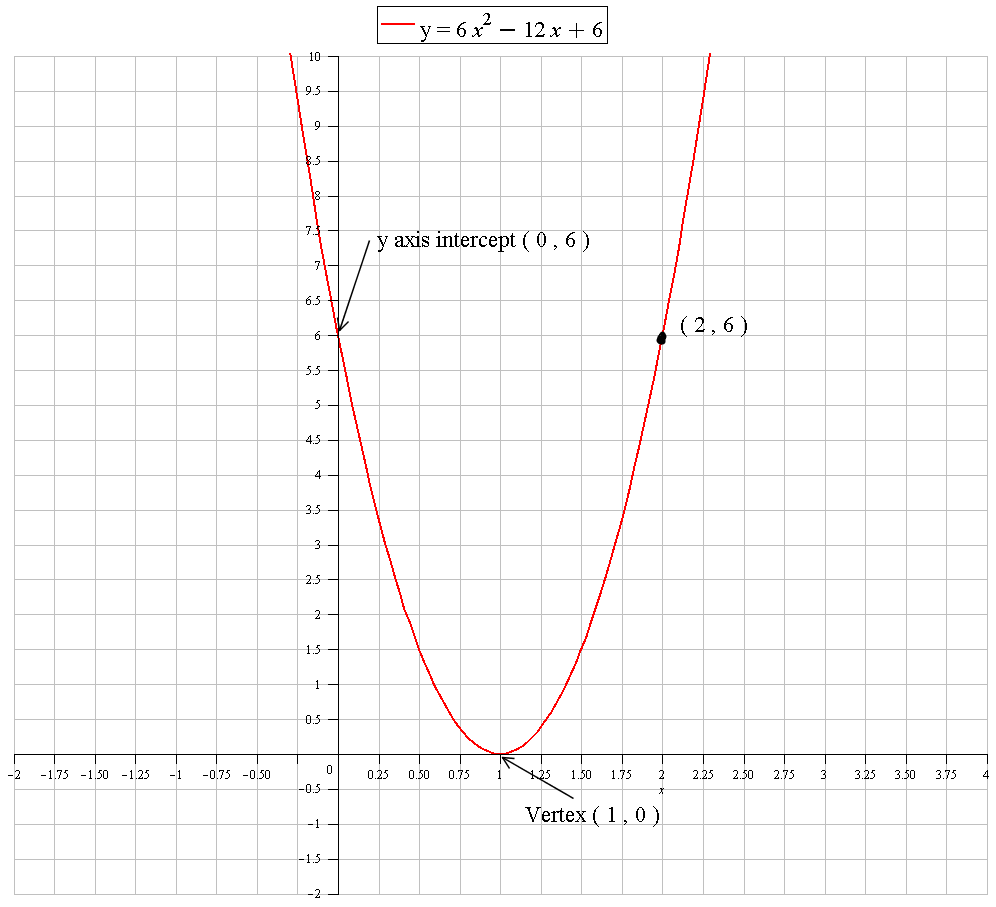
Find the vertex form of a quadratic that passes through (2,6), has an x-int of 1 and a y-int of 6?

I really don't get it, and that's all the info that's available

Answer 1

`color(blue)(y=6(x-1)^2)`

Explanation:

The vertex form of a quadratic equation of the form `color(red)(ax^2+bx+c=0)` is given as:

`color(red)(y=a(x-h)^2+k)`

Where:

`bba \ \` is the coefficient of `x^2`
`bbh \ \` is the axis of symmetry.
`bbk \ \` is the maximum or minimum value of the function.

From the given information it is possible to form three equation of the form:

`y=a(x-h)^2+k`

and solve these simultaneously. These will involve squared quantities and messy equations, so an easier method would be to find the quadratic in the form:

`ax^2+bx+c=0`

This will be much simpler:

We know it passes through the point `(2,6)` and has a y intercept of 6. The y intercept is the constant `bbc` in the standard form we will be using. We plug in this information to form the first equation.

`6=a(2^2)+b(2)+6=>4a+2b=0 \ \ \ \ \ [1]`

We have an `x` intercept of `1`, we know that at this value of `x`, `y=0` i.e. root of equation.

Plugging in these values along with `c=6` which we reasoned above.

`0=a(1)^2+b(1)+6=>a+b=-6 \ \ \ \ \ [2]`

Solving `[1]` and `[2]` simultaneously:

Multiply `[2]` by 2 and subtract from `[1]`

`4a+2b=0`
`2a+2b=-12`

`2a=12=>a=6`

Substituting this in `[2]`

`6+b=-6=>b=-12`

So we now have all the coefficients and constants of `ax^2+bx+c=0`

`a=6`

`b=-12`

`c=6`

`:.`

`6x^2-12x+6=0`

We still need this form: `y=a(x-h)^2+k`

It can be shown that:

`h=-b/(2a) \ \` and `\ \ \k=f(h)`

So we have:

`h=-(-12)/(2(6))=1`

`k=f(h)=f(1)=6(1)^2-12(1)+6=0`

In vertex form we get:

`y=6(x-1)^2`

This is its graph: