Find the interval and radius of convergence of the following power series (problem #1a)?
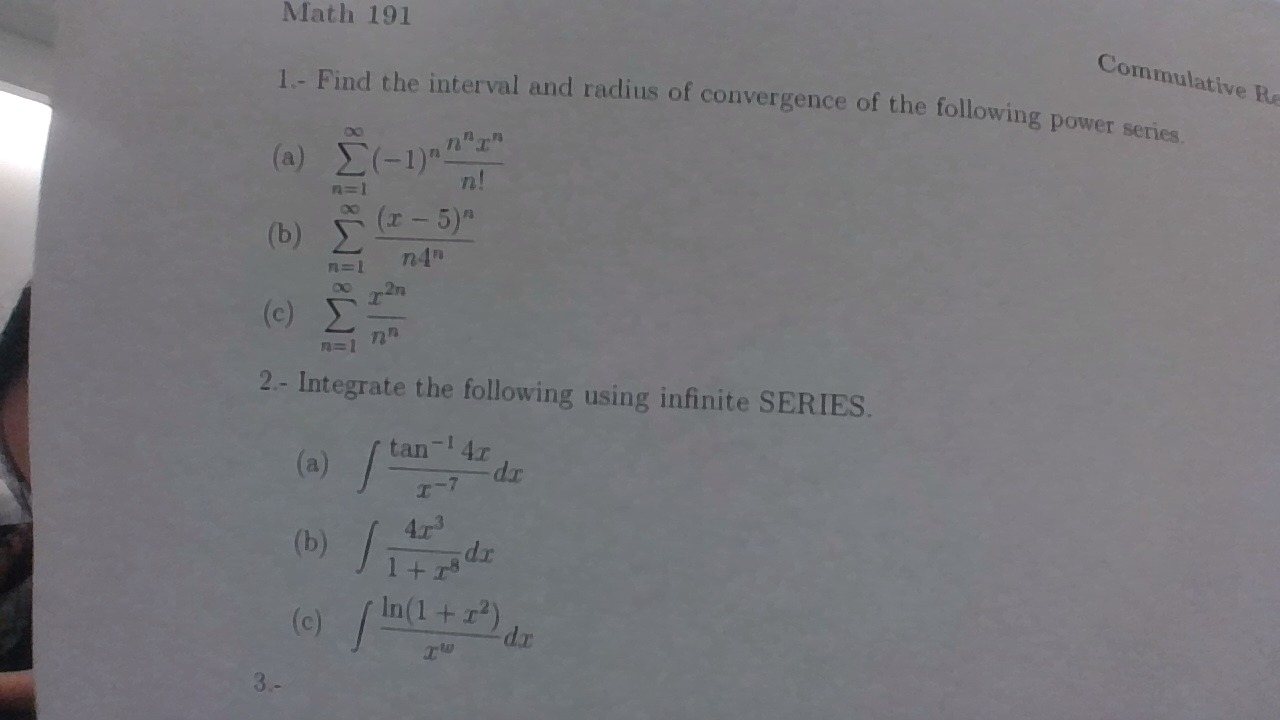
1 Answer
Use the ratio test to find the radius of convergence. You can then determine the interval from there.
#lim_(n->oo) ((-1)^(n + 1)(n + 1)^(n + 1)x^(n + 1))/(((n + 1)!)/(((-1)^n n^nx^n)/(n!))) < 1#
#lim_(n->oo) (-1(n + 1)^(n + 1)x)/((n + 1)n^n) < 1#
#lim_(n->oo) (-1(n + 1)^nx)/(n^n) < 1#
Let's consider the limit as
Thus
#|x|(e) < 1#
#|x| < 1/e#
So our interval of convergence will be
#(-1/e,1/e)#
However, we must test endpoints. When
#(-1)^n (n^n (-1/e)^n)/(n!)#
We can start by seeing that the negative bases will cancel and always give positives, so we can rewrite
#(n^n (1/e)^n)/(n!)#
Now we can write the first few terms down
#1/e + 2/e^2 + 9/(2e^3) + 32/(3e^4) + ...#
You can use the root test to see that this converges . As for
#(-1)^n (n^n(1/e)^n)/(n!)#
Write the first few terms down
#-1/e + 2/e^2 - 9/(2e^3) + 32/(3e^4) + ...#
This is an alternating series with terms approaching
Our interval of convergence is therefore
Hopefully this helps!

