Question

How do you find the domain and range of `f(x) = (x + 5)^2 + 8`?

Answer 1

`" "`
Domain: `color(blue)([-oo < x < oo ]`

Using Interval Notation: `color(blue)((-oo,oo)`

Range: `color(blue)([f(x)>=8 ]`

Using Interval Notation: `color(blue)([8,oo)`

Explanation:

`" "`
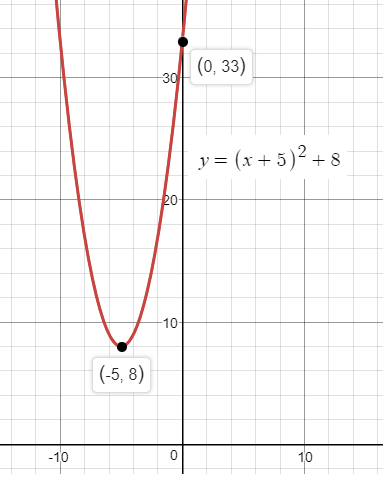
Given: `color(red)(y=f(x)=(x+5)^2+8`

The Vertex Form of a quadratic function is:

`color(green)(y=f(x)=a(x-h)^2+k`, where

`(h,k)` is the Vertex.

Note: `color(blue)(a=1, h=-5, k=8`

`color(green)("Step 1: "`

Vertex is at : `color(blue)((-5,8)`

Note :

If `a>0`, then the Vertex is a Minimum Value.

Since, `a=1`, the Vertex is `color(blue)("Minimum at "(-5,8)`

`"Range :"f(x)>= 8`

Using Interval Notation : `[8, oo)`

`color(green)("Step 2: "`

Find Domain :

Domain of `f(x)` is the set of all input values for which the given function is real and well-defined.

`color(blue)(f(x) = (x+5)^2+8` does not have any undefined points.

The function does not have any domain constraints.

Therefore domain is given by

`color(blue)(-oo < x < oo`

Using Interval Notation :

`color(blue)((-oo , oo)`

Hence, the required solutions are:
Domain: `color(blue)([-oo < x < oo ]`

Using Interval Notation: `color(blue)((-oo,oo)`

Range: `color(blue)([f(x)>=8 ]`

Using Interval Notation: `color(blue)([8,oo)`

`color(green)("Step 3: "`

Draw the graph of `color(red)(y=f(x)=(x+5)^2+8` to verify the solutions:

Hope it helps.