Please help me simplify. What is #cos^4theta -sin^4theta +sin^2theta# equal to?
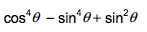
2 Answers
May 31, 2018
Explanation:
We have
Now we use that
So we get
May 31, 2018
Explanation:
#cos^4theta-sin^4theta" is a "color(blue)"difference of squares"#
#•color(white)(x)a^2-b^2=(a-b)(a+b)#
#"here "a=cos^2theta" and "b=sin^2theta#
#cos^4theta-sin^4theta=(cos^2theta-sin^2theta)(cos^2theta+sin^2theta)#
#[cos^2theta+sin^2theta=1]#
#cos^4theta-sin^4theta+sin^2theta#
#=cos^2theta-sin^2theta+sin^2theta#
#=cos^2theta#

