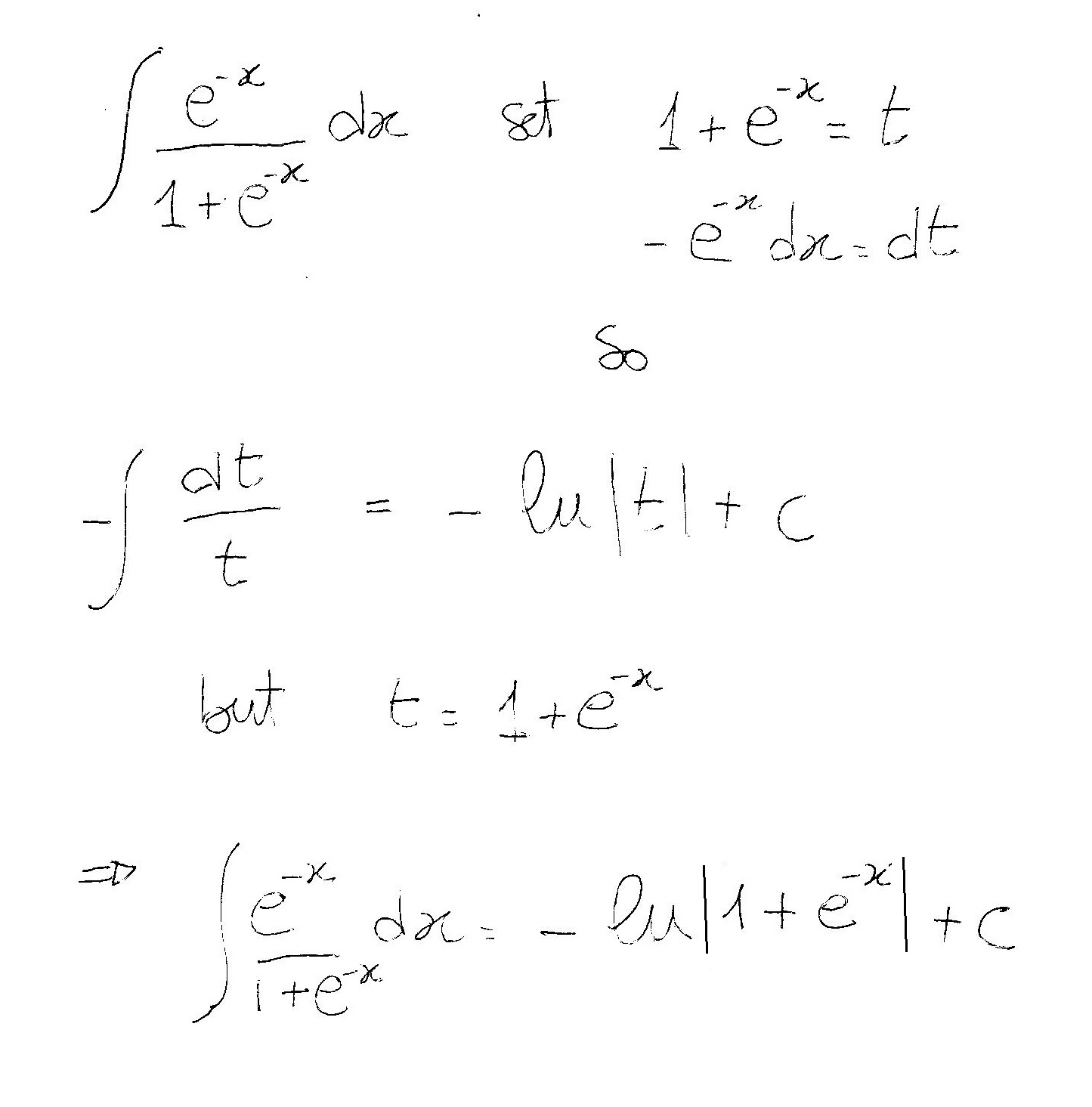How do you find int(e^-x)/(1+e^-x)dx?
4 Answers
Jun 28, 2018
Explanation:
ln(e^(-x)+1)=ln(1/e^x+1)=ln((e^x+1)/e^x)=ln(e^x+1)-lne^x=ln(e^x+1)-x
Therefore,
,
Jun 28, 2018
The answer is
Explanation:
Perform this integral by substitution
Let
Therefore, the integral is
Jun 28, 2018
Explanation:
Let
Rewrite
Substitute
This integral is
Substitute back
Jun 28, 2018
I tried this:
Explanation:
Have a look: