Question

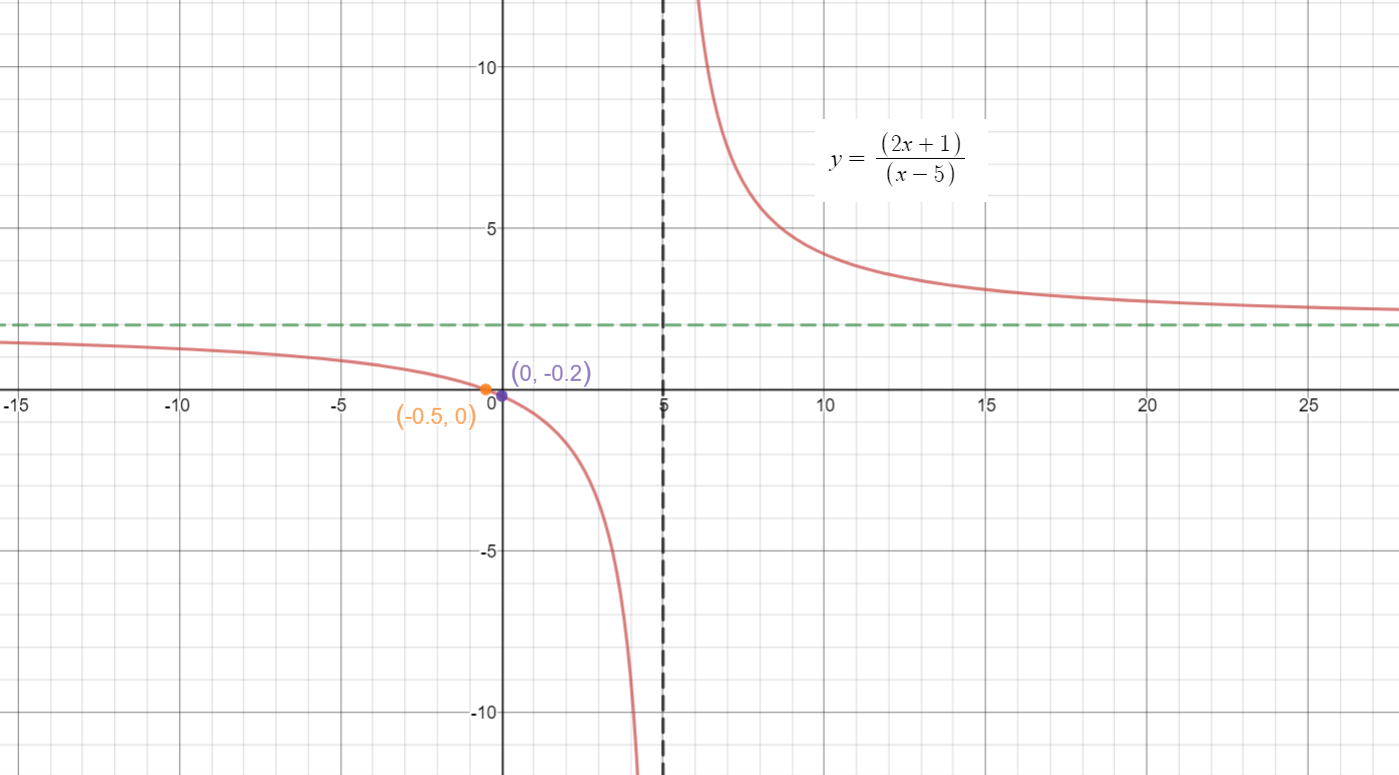
How do you graph `y =(2x + 1)/(x-5)`?

Answer 1

`" "`
Please read the explanation.

Explanation:

`" "`
Given:

Rational function : `color(red)(y=f(x)=(2x+1)/(x-5)`

`color(blue)("How do we graph a rational function ?"`

`color(green)("Step 1"`

Find both `color(red)(x and y` intercepts.

x-intercept:

Set `color(red)(y=0`

`rArr (2x+1)/(x-5)=0`

`rArr (2x+1)=0`

`rArr 2x=-1`

`rArr x=(-1/2)`

`color(red)("x-intercept": (-1/2,0)`

y-intercept:

Set `color(red)(x=0`

`rArr y=(2x+1)/(x-5)`

`rArr y=(2(0)+1)/((0)-5)`

`rArr y = 1/(-5)`

`color(red)("y-intercept": (0,-1/5)`

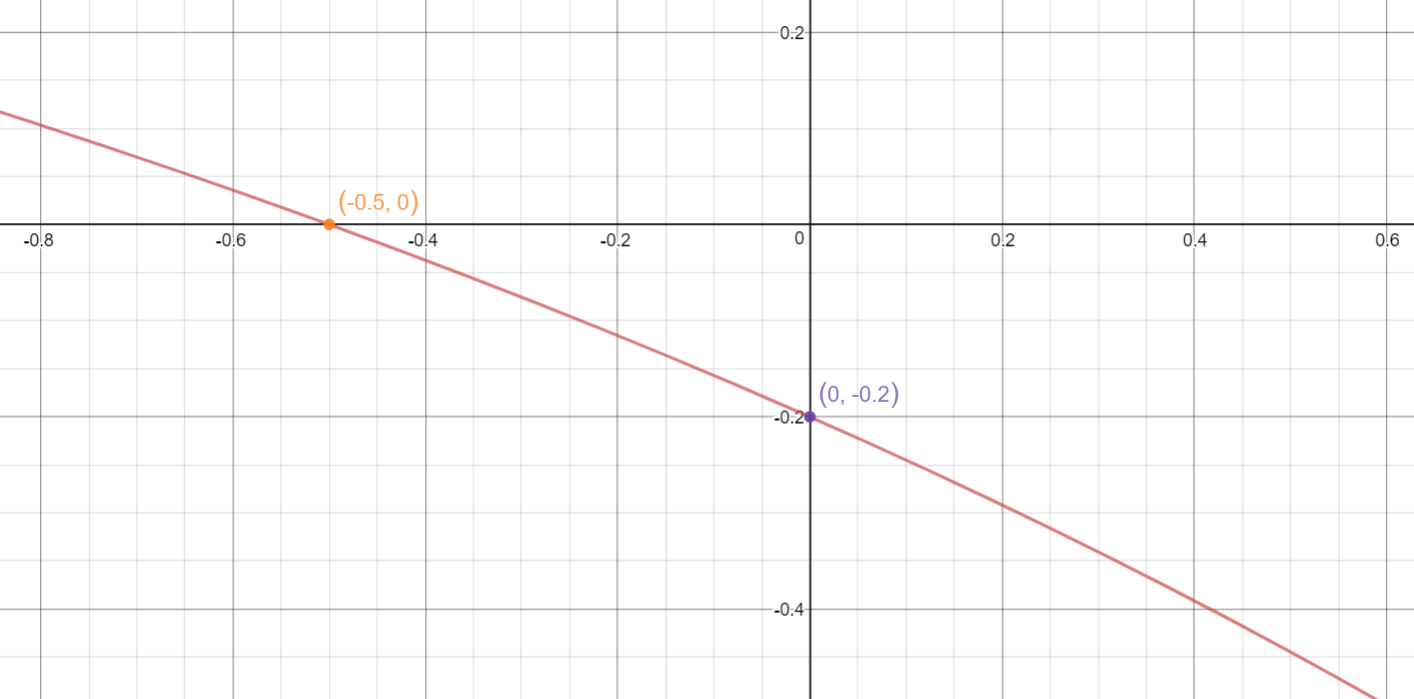
Both x and y intercepts are plotted in the graph above.

`color(green)("Step 2"`

Find Horizontal and Vertical Asymptotes

Vertical asymptotes are generated by the ZEROS of the denominator.

Horizontal asymptoes describe the behavior of the graph as the input values get larger or smaller.

Vertical asymptote:

Figure out what makes the denominator equal to zero.

Make sure that the numerator does not become zero for the same value.

`rArr (x-5)=0`

`rArr x=5`

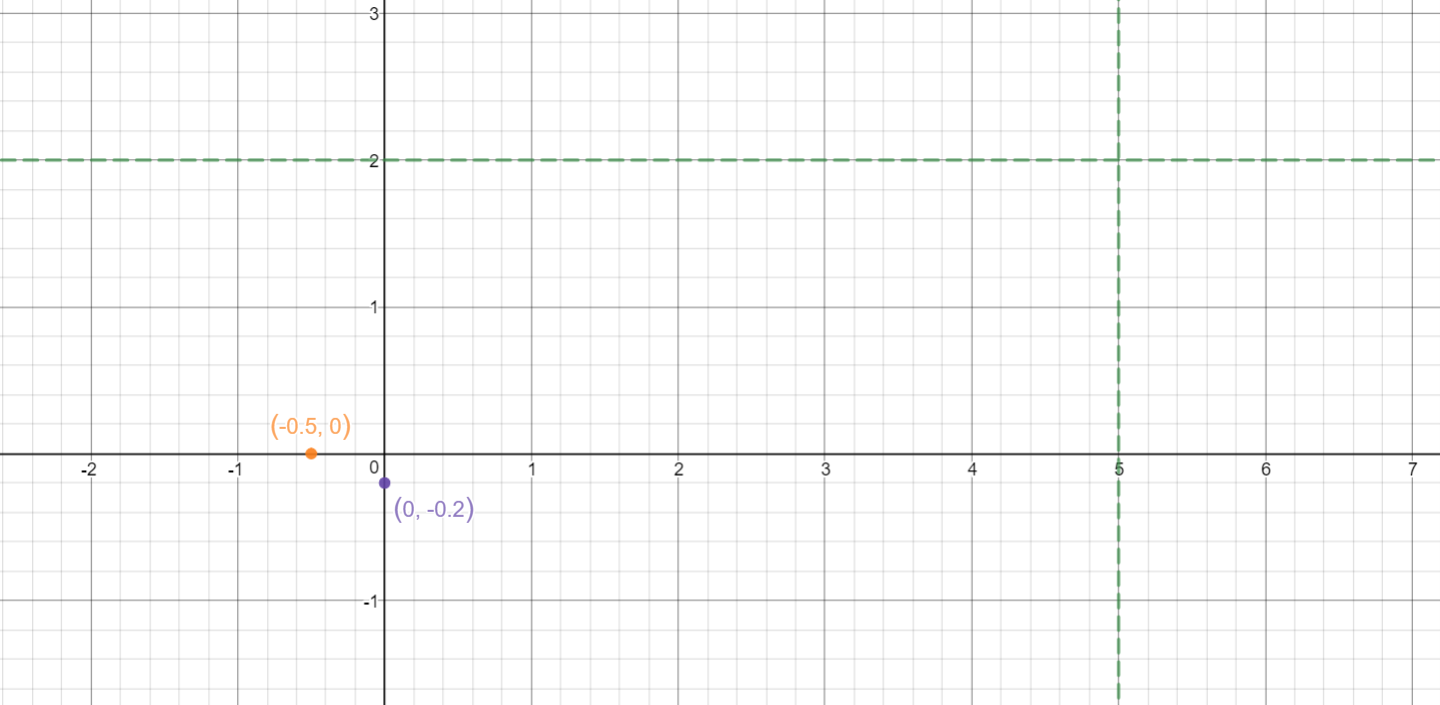
Vertical asymptote is at `color(red)(x=5`

Horizontal asymptote:

Numerator = `(2x + 1)`

Highest degree in both numerator and denominator is `color(red)(1`

`rArr 2/1=2`

Horizontal asymptote is at `color(red)(y=2`

You can view the asymptotes in the graph below:

`color(green)("Step 3"`

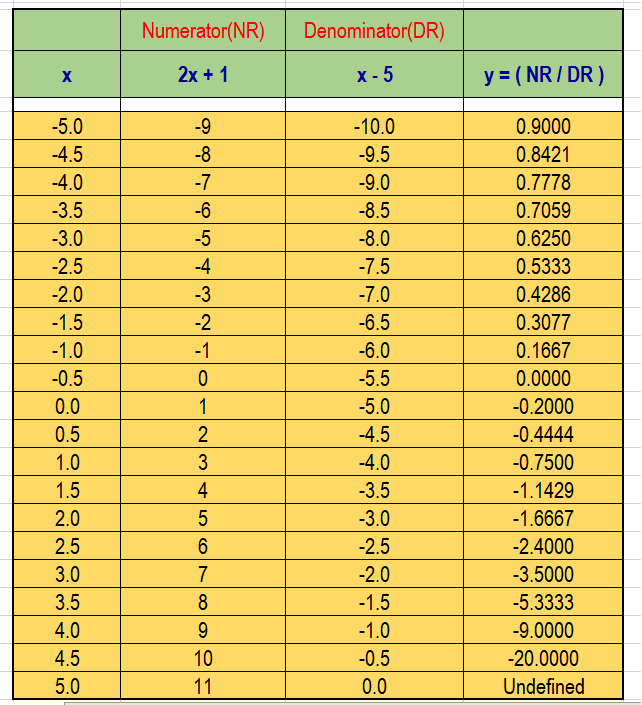
Generate a data table as follows:

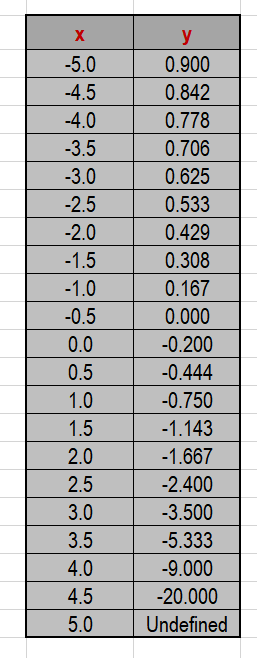
Consider the columns (first and the last): `color(blue)(x and y`:

`color(green)("Step 4"`

Graph:

Hope you find this useful.