Product of Power Series
Key Questions
-
One example that I find useful is the use and manipulation of the products of power series to derive
#e^(ix) = cosx + isinx# , which is an identity used many, many times to solve the Schroedinger Equation in Physical Chemistry, by substituting#i# for various different constants.
What is accepted by Physical Chemists is that you can write out the general solution to the Equation as:
#y(x) = c_1 e^(alphax) + c_2 e^(-alphax)# where
#alpha = iomegat# and, after various proofs and empirical tests, it is agreed that we can use#e^(alphax)# as a working "trial function" when we guess the form of the overall solution in terms of a finite addition of these#c*e^(alphax)# functions so that we can predict molecular properties:#psi(x) = sum_(i=1)^N c_i phi_i(x)#
where each#phi# could, for example, represent an atomic orbital, and#psi(x)# would in that case be the molecular orbital.A common example of solving the time-dependent Schroedinger equation is (example 2-4 in Physical Chemistry: A Molecular Approach):
#(d^2x(t))/(dt^2) + omega^2x(t) = 0# subject to the boundary conditions
#x(0) = A# and#(dx(0))/(dt) = 0# . These boundary conditions define the fact that a stationary transverse wave with one antinode has two endpoints, and these are at#x = 0# and#x = l# , half of the wavelength.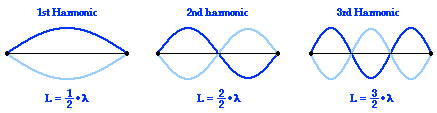
To solve this one, one would have to use identity written at the top, with
#alpha# substituted for#i# like so:#c_1e^(alphax) + c_2e^(-alphax)# #= c_1(cosx + alphasinx) + c_2(cosx - alphasinx)# #= c_1cosx + c_1alphasinx + c_2cosx - c_2alphasinx# #= (c_1 + c_2)cosx + (c_1alpha - c_2alpha)sinx# and it is generally written out by absorbing the arbitrary constants
#c_1# ,#alpha# , and#c_2# into new arbitrary constants#c_3# and#c_4# , with#c_1 + c_2 = c_3# and#c_1alpha - c_2alpha = c_4# :#= c_3cosx + c_4sinx# Then, substituting
#omegat# for#x# , we get:#c_3cos(omegat) + c_4sin(omegat)# for the solution to the so-called common example.
Looking at the boundary condition
#(dx(0))/(dt) = 0# , we get:#= c_3(-sin(omegat))*omega + c_4cos(omegat)*omega# #= cancel(c_3(-sin(omega(0)))*omega)^(0) + c_4cos(omega(0))*omega# #= c_4omega# But we know that at
#t = 0# ,#omega = 0# because time has not passed yet.#=> c_4omega = 0# , thus satisfying the condition#(dx(0))/(dt) = 0# .Using the
#x(0) = A# boundary condition we get:#x(0) = c_3cos(omega(0)) + cancel(c_4sin(omega(0)))^(0)# #= c_3# with
#c_3# taken as#A# ---which is the amplitude of an initialized stationary wave---since it is the only contributor to the wave. Thus, since#c_3 = A# , we have satisfied the condition#x(0) = A# , and we just have:#color(blue)(x(t) = Acos(wt))# which is the familiar physics equation for a transverse wave, as depicted in the image above! :)
-
#(sum_{n=0}^infty a_nx^n)cdot(sum_{n=0}^infty b_nx^n)=sum_{n=0}^infty(sum_{k=0}^na_kb_{n-k})x^n# Let us look at some details.
#(sum_{n=0}^infty a_nx^n)cdot(sum_{n=0}^infty b_nx^n)# by writing out the first few terms,
#=(a_0+a_1x+a_2x^2+cdots)cdot(b_0+b_1x+b_2x^2+cdots)# by collecting the like terms,
#=a_0b_0x^0+(a_0b_1+a_1b_0)x^1+(a_0b_2+a_1b_1+a_2b_0)x^2+cdots# by using sigma notation,
#=sum_{n=0}^infty(sum_{k=0}^na_kb_{n-k})x^n#
Questions
Power Series
-
Introduction to Power Series
-
Differentiating and Integrating Power Series
-
Constructing a Taylor Series
-
Constructing a Maclaurin Series
-
Lagrange Form of the Remainder Term in a Taylor Series
-
Determining the Radius and Interval of Convergence for a Power Series
-
Applications of Power Series
-
Power Series Representations of Functions
-
Power Series and Exact Values of Numerical Series
-
Power Series and Estimation of Integrals
-
Power Series and Limits
-
Product of Power Series
-
Binomial Series
-
Power Series Solutions of Differential Equations