Translations of Sinusodial Graphs

Key Questions

How do I find the phase shift of a sinusoidal graph?

Answer:

Find the value of #x# at which we find #sin(0)#.

Explanation:

Examples:

#y=3+2sin(3x- pi/4)#

Solve: #3x-pi/4 = 0#

So #x= pi/12# is the shift.

#y=5-sin(4x+ pi/2)#

Solve: #4x + pi/2 = 0#

So #x= -pi/8# is the shift.

#y=-3sin(pix+ (3pi)/4)#

Solve: #pix + (3pi)/4 = 0#

So #x= -3/4# is the shift.

Some textbooks use:
#y = asin(bx+c)# has phase shift #-c/b#

Other textbooks use:
#y = asin(bx-c)# has phase shift #c/b#

For me (having taught out of both kinds of textbook), it's easier just to solve the equation.

Jim H · 1 · Jun 19 2015
What are sinusoidal graphs?

Answer:

A graph which follows the sine ( or is derivative) function, or simply put a graph which increases in value and then decreases in value periodically. Something like a wriglly snake.

Explanation:

graph{sin(x) [-10, 10, -5, 5]}
This graph for Sin(x)

graph{sin(x) + sin(2x) [-10, 10, -5, 5]}

This is graph for Sin(x) + Sin(2x)

graph{sin(x) +5 [-20, 20, -10, 10]}

This is graph for Sin(x) +5

devi f. · 1 · Mar 8 2018
How do I find the equation of a sinusoidal graph?

Answer:

I will provide you with two examples.

Explanation:

Before we get to problems, I would like to go through a little bit of vocabulary.

•A sinusoidal function is a function in sine or in cosine

•The amplitude of a graph is the distance on the y axis between the normal line and the maximum/minimum. It is given by parameter #a# in function #y = asinb(x - c) + d or y = acosb(x - c) + d#

•The period of a graph is the distance on the x axis before the function repeats itself. For sinusoidal functions, it is given by evaluating #(2p)i/b# in #y = acosb(x - c) + d or y = asinb(x - c) + d#

•The horizontal displacement is given by solving for #x# in #x - c = 0# in #y = acosb(x - c) + d or y = asinb(x - c) + d#. The horizontal displacement means the number of units right or left in from the x axis

•The vertical displacement is given by #d# in #y = acosb(x - c) + d or y = asinb(x - c) + d#. The vertical displacement is the displacement up or down from the y axis.

This being done, we can now look at a few applications to these particular words.

Example 1:

What is a cosine equation for the following graph?

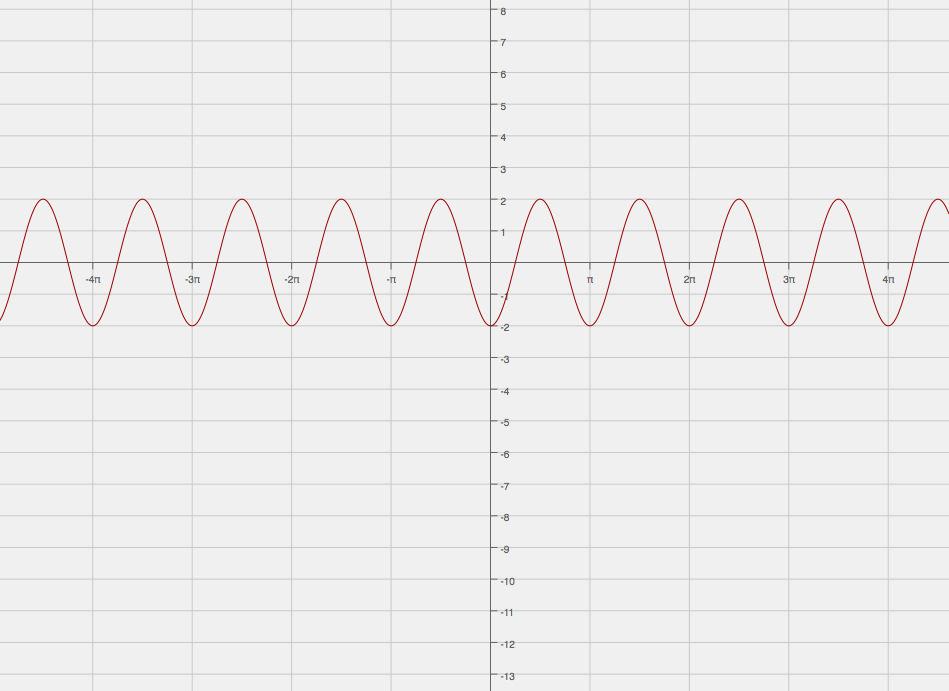
First, let's note the amplitude. The normal line is the line that runs completely in the middle, so it is #x = 0#. This also signifies that there is no vertical displacement, or #d = 0# in #y = acosb(x - c) + d#.

The amplitude is given by #"equation of max" - "equation of normal"#. In this case, the equation of the maximum is #y = 2# while the equation of the normal is #y = 0#. Hence, the amplitude is #2 - 0 = 2#.

However, the graph of #y = cosx# has a maximum on the y axis, not a minimum like in our graph. What does this signify? It signifies there has been a reflection over the x axis, which means parameter #a# is negative. Hence, parameter #a# is #-2#. Note that the amplitude can never be negative, so it's given by #|a|#.

Next, let's determine the period. Look back at the definition above of "period". It is the distance between two maximums or two minimums. In the graph above, the distance between any two maximums or minimums is #pi#. We know the period now, all that remains is to find the value of #b#.

Recall the period of a sinusoidal function is given by #(2pi)/b#. Hence, we can state that #(2pi)/b = pi#

Solving for b:

#2pi = bpi#

#(2pi)/pi = b#

#b = 2#

So, #b = 2#.

As for horizontal displacements, there are none, since the minimum is on the y axis; it hasn't been moved left or right.

In summary, we can now state that the equation of the function above is #y = -2cos(2x)#.

Example 2:

Determine the equation of the following graph.

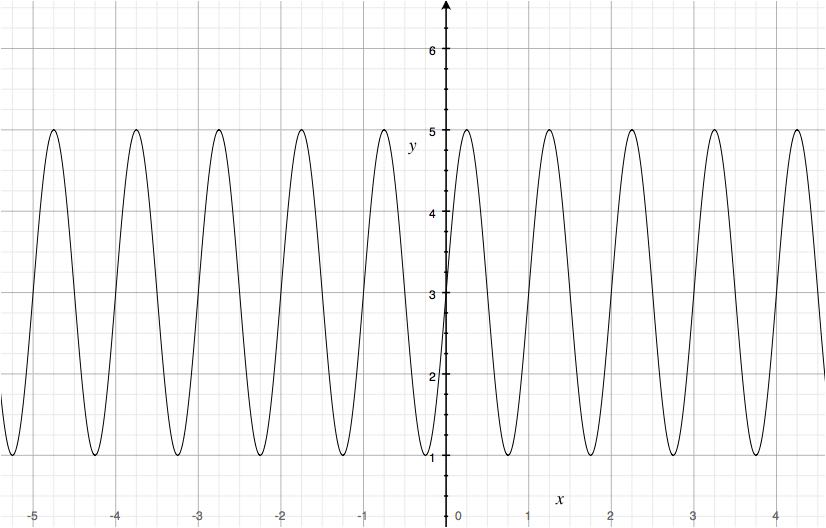
This is a little more complicated. We first note that a vertical displacement has occurred. The graph has been moved upwards #3# units relative to that of #y = sinx# (the normal line has equation # y = 3#). We can also conclude that this is a sine function, because the graph meets the #y# axis at the normal line, and not at a maximum/minimum.

As for the amplitude, we find the maximum is at #y = 5# while the normal line is #y = 3#. Hence, the amplitude is #5 - 3 = 2#.

This graph has undergone no reflection over the x axis, so parameter #a# is positive in this scenario.

As for the period, the distance between all two maximums and minimums is #1#, so the period is #1#. We must determine the value of #b#:

#(2pi)/b = 1#

#2pi = b#

Hence, #b = 2pi#.

Finally, we need to determine the factor of the horizontal displacement. We find that it is #1# unit to the right. Hence, our equation is #y = 2sin(2pi(x - 1)) + 3#.

Hopefully this helps!

Noah G · 1 · Jul 12 2016
How do I graph sinusoidal functions?

Answer:

See explanation.

Explanation:

We know what the basic graph of #y = sinx# look like.

graph{y = sinx [-12.11, 16.36, -6.92, 7.31]}

The graph goes up to a maximum of #1# and down to a minimum or #-1#. It is 'centered' on the #x# axis which is the line #y=0#.

Let's look at: #f(x) = D+Asin(Bx+C)#

The number #D# will shift the entire graph up (if #D > 0#) or down (#D < 0#) by the amount #absD#
If #D != 0#, the center line will move to the horizontal line: #y = D#

Let's leave that vertical shift out and just look at:

#y = Asin(Bx+C)#

If #B < 0#, use the fact that #sin(-u) = -sin(u)# to rewrite with a positve coefficient of #x#.

If #A# is negative, we will reflect the graph across the #x# axis.

Multiplying the sine by #A# makes the new graph have a maximum of #absA# and a minimum of #-absA#.
The number #absA# is called the Amplitude of the graph.

The period of the graph is the length of one complete cycle through the graph. For the basic graph, the period is #pi#.
We often think of and describe this by saying, "The first period of the graph starts when we take the sine of #0# and ends when we take the sine of #2pi#. That means the angle has gone once around the circle."
(This description is helpful, but can be a little misleading, too.)

Returning to #y = Asin(Bx+C)#

We will take the sine of #0# when #Bx+C = 0#
and we will take the sine of #2pi# when #Bx+C = 2pi#

So we will start the first period when #x = -C/B# (solve the first equation.)
The number #-C/B# is called the Phase (or Horizontal) Shift.

And we will finish the first period when #x = (2pi-C)/B# (Don't memorize that, we have another way of finding it.)

The "length of the period" is the end minus the start, or:

#((2pi-C)/B) - (-C/B)# And that simplifies to #(2pi)/B#

So that is the why, and here is the summary:

#y = Asin(Bx+C)# has

Amplitude: #" "absA" "# (That's how far above and below the center line we need to go.)

Period: #" "(2pi)/B" "#

Phase Shift: #" "# Is the solution to #Bx+C = 0#

Jim H · 1 · Aug 2 2015