Question #6390e
1 Answer
It means that a planet does not necessarily compensate due to its distance from the sun, making "life conditions" (i.e. day and night, seasons) different in different planets.
Explanation:
Third law of Kepler : The square of the orbital period of a planet is proportional to the cube of the semi-major axis of its orbit [1].
So, the first to see is that the law is applied for planets, not for a single planet, it serves to understand differences between planets, not a single planet.
We have, mathematically:
Where:
In order to understand it, let's take an example:
Use:
Do the math and find it:
So, the planet is twice farther, but its period is just about 1.41 faster, the year is longer than expected, less sun in the cold days, and too much sun in the hot days. For us it is fatal, just a little bit of sun this years in Italy was serious, people started to get sick, mainly elderly ones.
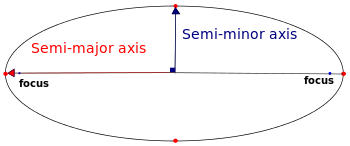 [2]
[2]
PS. it has been more than five years I have "taught" physics, thus, I would ask to someone kindly review the math and physics.
[1] https://en.wikipedia.org/wiki/Kepler%27s_laws_of_planetary_motion. Accessed on 22 nov 2015.
[2] https://en.wikipedia.org/wiki/Semi-major_axis Accessed on 22 nov 2015.

