Kepler's Laws
Key Questions
-
Equal areas are swept by a line segment joining a planet and the Sun in equal intervals of time.
Kepler's second law states that the time an object in an elliptical orbit takes to go from a point
#P# of the orbit to a point#Q# of the orbit is proportional to the area defined by the line segments joining the points to one of the focci of the ellipse and by the trajectory of that object.A more concrete example would be the motion of the Earth around the Sun. Aproximating Earth's orbit to a circle (it can be show that's not a bad approximation), with the Sun being in the center, Kepler's second law guarantees that the time it takes for Earth to travel a certain distance is always the same, for:
The radius of the circle is a constant
#r# If the distance traveled by Earth in the process of going from point#P_1# to the point#Q_1# is#s# , and the distance traveled in the process of going from point#P_2# to the point#Q_2# is also#s# , then the shapes defined by the line segments (radii of the circle) joining those points to the Sun and by the trajectory of the motion is a sector of the circle. Since the area#A# of the sector of a circle is given by the relation#A=pi r^2 theta# , where#theta# is the angle (in radians) definied by the line segments, and the angle itself is defined as#theta = s/r# , we get#A=pi r s# . Since#s# is the distance considered for both trajectories, the area "swept" by them is the same, and therefore, by Kepler's second law the time intervales expended in those trajectories are the same.It must be noted that, while Kepler deduced the three famous laws of orbital motion from observations, they can be proved if one assumes that Newton's law of gravitation is valid.
-
Kepler's third law states that the ratio of the square of the period of a planets orbit to the cube of its rotational distance from the sun is the same for all planets. That's a long winded way to say that;
#T^2/R^3 = # the same for all of the planetswhere
#T# is the time it takes a planet to orbit the sun once, and#R# is the average distance from the sun. Kepler discovered his laws empirically, meaning that he looked at his data and noticed certain patterns. To understand why it works, we can derive this law based on physics.First off, Kepler's first law states that the planets' orbits are ellipses, with the sun at one focus. They are, however, nearly circular, so for simplification, lets assume that the orbits are circles. We'll start by combining Newton's law of gravitation and Newton's second law;
#F=G(Mm)/R^2# (law of gravity)#=ma# (2nd law)
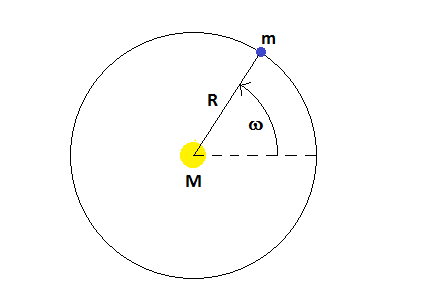
Here,
#G# is Newton's gravitational constant;#M# is the mass of the sun;#m# is the mass of the planet;#R# is the distance the planet orbits from the sun; and#a# is the acceleration of the planet toward the sun. Right away we can see that#m# is irrelevant to our calculation so we can remove it.#GM/R^2 = a# (equation 1)For an object moving at constant speed in a circle, the acceleration toward the center of that circle is given by;
#a = omega^2 R# where
#omega# is the rotational velocity, measured as the radial distance the planet moves over time. Since the total radial distance is#2pi# , the number or radians in a circle, and the total time is one period,#T# , we can replace#omega# with#(2pi)/T# to get;#a = ((2pi)/T)^2R# so that equation 1 becomes;
#GM/R^2 = ((2pi)/T)^2R# We can now move all of the variables to one side and the constants to the other to get Kepler's third law.
#T^2/R^3 = (4(pi)^2)/(GM) =# ConstantThe only thing that effects this constant is the mass of the sun. For larger stars, the ratio becomes smaller, meaning that the period decreases for a planet orbiting the same distance from the star.