Boyle's law states that the pressure and the volume of a gas are proportional to one another, if temperature and the number of moles are kept constant.
Starting from the ideal gas law, #PV = nRT#, and taking into account the premise that moles and temperature are kept constant, we get
#V = 1/P * nRT -> V = 1/P * k#, where
#k = nRT = const ant#
Now, a plot of #V# vs #1/P# will look like this (the graph on the right)
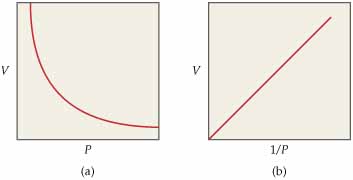
Notice that the line starts from the origin, which is consistent with the premise that #b=0 -># from #y = mx +b#
SInce your linear equation is given,
#y= 2060.1x + 2*10^(-5)#, we can assume that #2*10^(-5)# is negligible; all you need now is a second point on the line in order to express the slope. The most obvious point on this graph is #(0,0)#, which will give
#m = (y_1 - y_2)/(x_1 - x_2) = (3.1146 - 0)/(0.001526618 - 0) = 2040.2#, which represents the slope of the graph #V# vs #1/P#, and the constant #k = nRT#.

