In the beginning of this answer, I will be fussy (sorry, I'm a mathematician...).
Every line on a plane is parallel to a diameter of a circle lying on the same plane. In fact, a circle doesn't have the diameter, but it has infinitely many diameters. So the object "a parallel to the diameter" is every line of the plane.
Another fussiness about this question is the word "between", because the two shapes (line and circle) do not necessarily surround a closed area: if the line doesn't cross the circle, you have to specify how to enclose this area.
However, the words "cup shape" made me think that you want to find out how to calculate the area of a so-called circular segment:
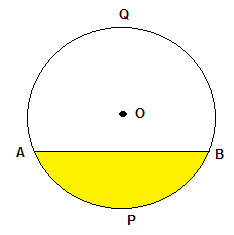
The area of the "cup shape" is given by the area of the circular sector #s=OAPBO# minus the area of the triangle #Delta=Delta(AOB)#. They both depend on the angle #alpha=hat{AOB}#. Given the radius #r=AO=BO=PO# of the circle, the area of the triangle #Delta(AOB)# is given by the triangle area formula:
#A_{Delta}= 1/2 bar{AO} * bar{BO} sin alpha=1/2 r^2 sin alpha#
The area #A_s# of the circular sector is directly proportional to the angle #alpha#, so we can use the proportion #A_s / alpha = {pi r^2} / {2 pi}# to get:
#A_s=1/2 r^2 alpha#
So the area we're searching for is #A=A_{s}-A_{Delta}=1/2 r^2 (alpha - sin alpha)#.
We can also use the height #h# of our "cup" (i.e. distance between the point #P# and the segment #bar{AB}#) to express the angle #alpha#. If #bar{OH}# is the height of the triangle #Delta(AOB)#, then #bar{OH}=r-h#. The height #bar{OH}# is also the bisector of the triangle #Delta(AOB)# (it's an isosceles triangle). That is: #hat{AOH}=alpha /2#.
Now let's consider the triangle #Delta (AOH)#: it's a right triangle, so by definition of cosine we get #bar{OH}=bar{AO} cos(hat{AOH})=r cos(alpha/2)#. So #cos(alpha/2)=bar{OH}/r# and this means that #cos(alpha/2) = {r-h}/r=1-h/r# and #alpha=2 arccos(1-h/r)#.
We finally get the following (awful) formula:
#A=1/2 r^2 (2 arccos(1-h/r)-sin(2 arccos(1-h/r)))=1/2 r^2 (2 arccos(1-h/r)-2sin(arccos(1-h/r)) cos(arccos(1-h/r)))=r^2 (arccos(1-h/r)-sqrt(1-(1-h/r)^2) (1-h/r))=r^2 (arccos(1-h/r)-sqrt(h/r(2-h/r)) (1-h/r))#.
Note:
We used the following two formulas
#sin(2x)=2 sin x cos x#
#arccos(sin(x))=sqrt{1-x^2}#

