Area of a Triangle
Key Questions
-
Heron's formula allows you to evaluate the area of a triangle knowing the length of its three sides.
The area#A# of a triangle with sides of lengths#a, b# and#c# is given by:#A=sqrt(sp×(sp-a)×(sp-b)×(sp-c))# Where
#sp# is the semiperimeter:#sp=(a+b+c)/2# For example; consider the triangle:
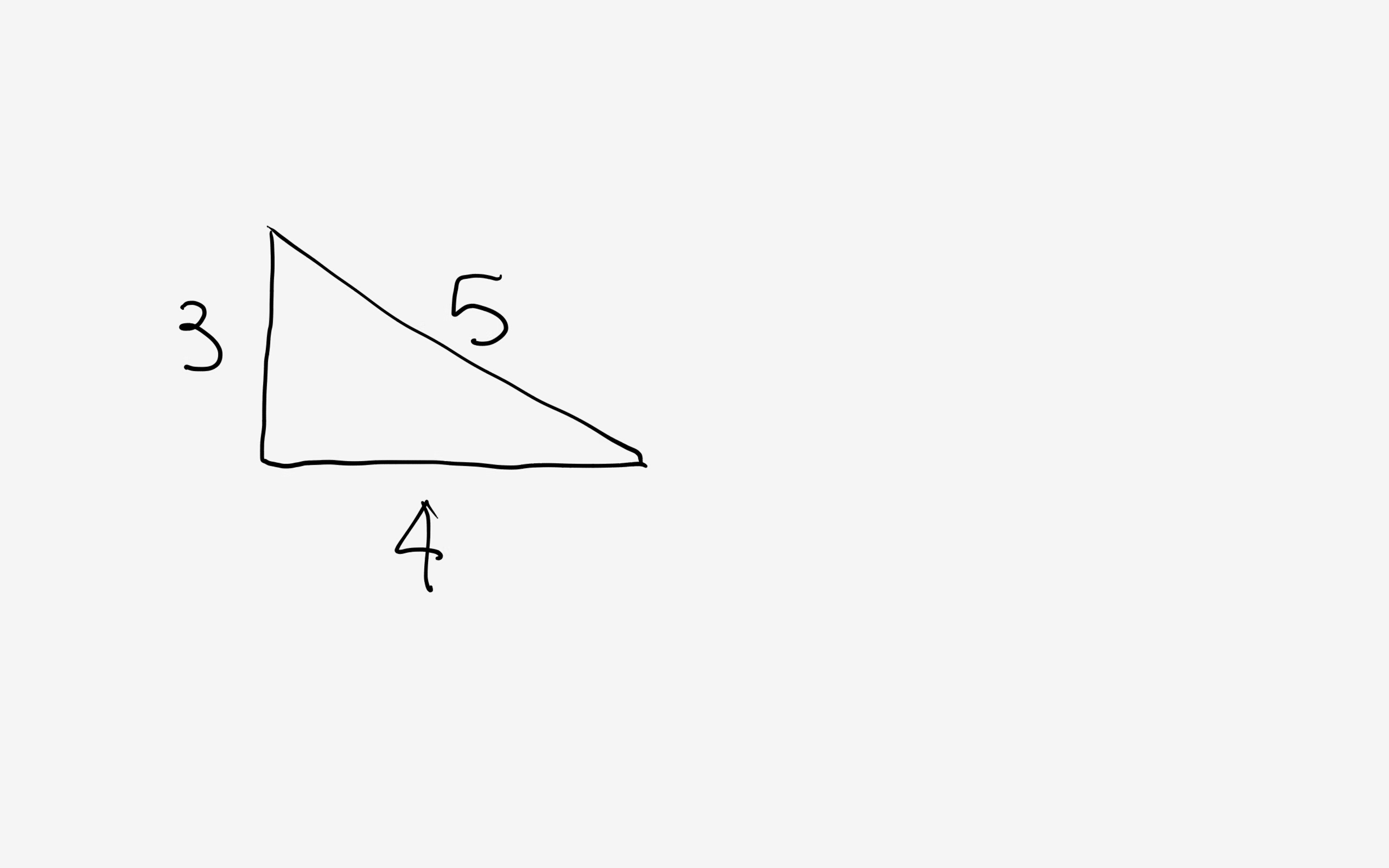
The area of this triangle is#A=(base×height)/2#
So:#A=(4×3)/2=6#
Using Heron's formula:
#sp=(3+4+5)/2=6#
And:
#A=sqrt(6×(6-5)×(6-4)×(6-3))=6# The demonstration of Heron's formula can be found in textbooks of geometry or maths or in many websites. If you need it have a look at:
http://en.m.wikipedia.org/wiki/Heron%27s_formula -
You can use it whenever you know the lengths of all three sides of a triangle.
I hope that this was helpful.