Question

Question #b94a3

Answer 1

(wikipedia)

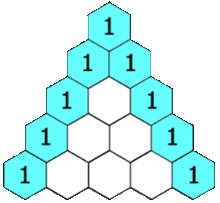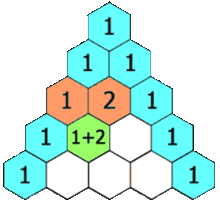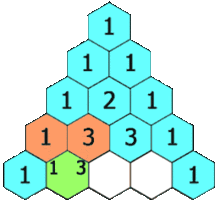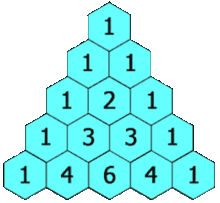
The Pascal triangle gives the coefficients for each term of the expansion of `(a+b)^n` by taking the `nth` row of the triangle (the top `1` is not counted).

Example :
`(a+b)^2=(1)*a^2+(2)*a^1b^1+(1)*b^2`

In your case you would have to be aware that the `b` above must be substituted by `2y` (and the `a` by `x` of course). We use the `4th` row, which is the bottom row in the picture:

`1*x^4+4*x^3(2y)+6*x^2(2y)^2+4*x(2y)^3+1*(2y)^4`

`=x^4+8x^3y+24x^2y^2+32xy^3+16y^4`

You will notice that the exponents of the first term (`x`) go down from `4` to `0` and those of the second term (`2y`) go up from `0` to `4`