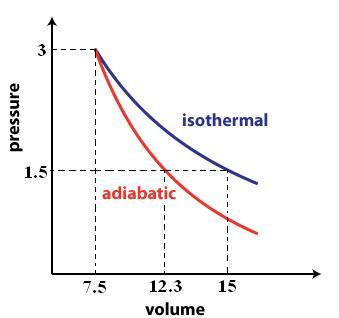
When you compress a gas isothermally, you're essentially keeping the temperature constant. When temperature and number of moles are kept constant, you use Boyle's Law to solve for the volume of the gas after the compression.
#PV = "constant"#
or
#P_1V_1 = P_2V_2#, where
#P_1#, #V_1# - the pressure and volume at an initial state;
#P_2#, #V_2# - the pressure and volume at a final state.
#V_2 = P_1/P_2 * V_1 = (1.5cancel("atm"))/(3cancel("atm")) * "15 L" = color(green)("7.5 L")#
An adiabatic expansion implies that the gas is thermally isolated from its surroundings, which implies that temperature will no longer be constant.
That happens because the gas will now do work on its environment, which will affect its internal energy and change its temperature.
The equation you'll now use is
#PV^(gamma) = "constant"#
or
#P_1V_1^(gamma) = P_2V_2^(gamma)#, where
#gamma# - the adiabatic index - calculated using the degrees of freedom of the gas(a value of 1.4 corresponds to a diatomic gas).
Solving for #V_2# will get you
#V_2^(gamma) = P_1/P_2 * V_1^(gamma) = (3cancel("atm"))/(1.5cancel("atm")) * 7.5^1.4 = 33.5827#
#ln(V_2^(gamma)) = ln(33.5827) => gamma * ln(V_2) = 3.514#
#ln(V_2) = 3.514/1.4 = 2.51#
#V_2 = e^2.51 = color(green)("12.3 L")#
To solve for the final temperature of the gas, use the equation
#T_1V_1^(gamma-1) = T_2V_2^(gamma-1)#
#T_2 = (V_1/V_2)^(gamma-1) * T_1 = ((7.5cancel("L"))/(12.3cancel("L")))^(1.4-1) * (273.15 + 20)"K"#
#T_2 = color(green)("241 K")#
A rough sketch of the P vs. V graph would look like this