What is the difference between the cross-product and the dot-product of two vectors? or If a force of 10 Newtons at an angle of #30^circ# above horizontal is used to drag a block 6 meters, how much work is done?
2 Answers
The Cross Product is a vector
If A and B are vectors
then
where
and
The Dot Product is a scalar
If A and B are vectors such that
and
then
it can also be evaluated as
where
Work is a dot product.
It is given as:
Where:
The result is a SCALAR (basically a quantity without vectorial characteristics) and is measured in Joules (J).
To evaluate it you do:
where you multiply the modulus of your vectors times the cosine of the angle between them.
For example:
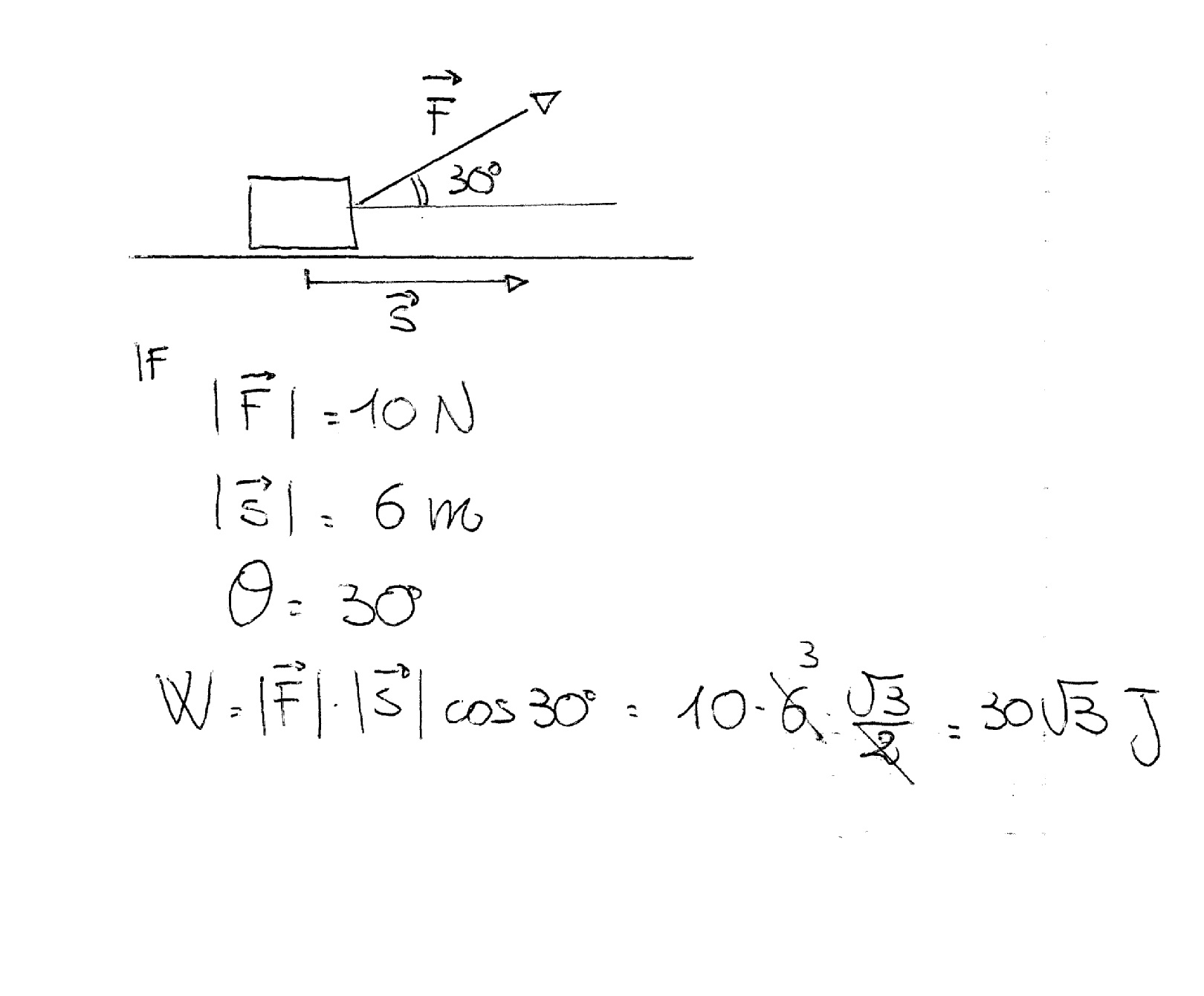
Hope it helps.

