The answer is A) V^(2+), U^(3+), Y^(3+).
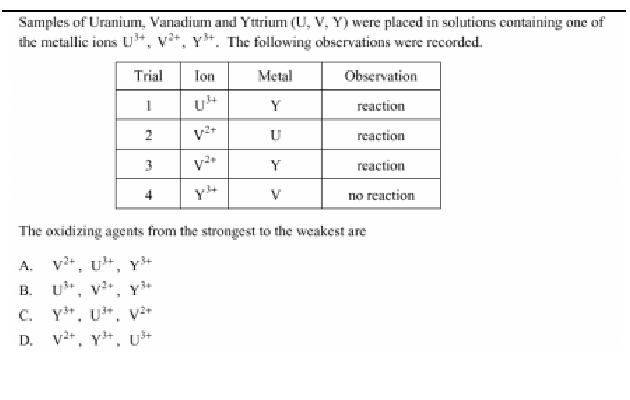http://imgur.com/k2U2nNq
I'll give you the quick answer first, then focus more on explaining what's going on.
Right from the get-go, you can sahy that Y^(3+) wil be the weakest oxidizing agent. If you only use the information given to judge each cation's oxidizing strength, the fact that Y^(3+) cannot oxidize U placed it at the bottom of the stack.
By comparison, U^(3+) can oxidize one species, Y, and V^(2+) can oxidize two species, U and Y.
So there you have it
V^(2+) > U^(3+) > Y^(3+)
Now, here's what's going on. Since we've been working with standard electrode potentials, you can write the reduction half-reactions for U, V, and Y
U^(3+) + 3e^(-) rightleftharpoons U, E_U^@
V^(2+) + 2e^(-) rightleftharpoons V, E_V^@
Y^(3+) + 3e^(-) rightleftharpoons Y, E_Y^@
So, you start by placing Y in a solution that contains the U^(3+) cation and you observe that a reaction takes place. This means that U^(3+) oxidizes Y.
Automatically, E_U^@ must be more positive than E_Y^@, since U^(3+) can take electrons from Y. Keep this in mind
E_U^@ > E_Y^@
Now you place U in a solution that contains V^(2+) cations and you observe that a reaction takes place. The same thing that happensed before happens again.
V^(2+) oxidizes U, which must mean that
E_V^@ > E_U^@
Moving on. You place Y in a solution that contains V^(2+) cations, and the same thing happens again. V^(2+) oxidizes Y, which implies that
E_V^@ > E_Y^@
Finally, you place V in a solution that contains Y^(3+) and observe that the two don't react. This means that Y^(3+) cannot oxidize V, so
E_V^@ > E_Y^@
As you can see, it all comes down to solving the famous "if A is greater than B, and B is greater than C" inequalities. If you have
{ (E_U^@ > E_Y^@), (E_V^@ > E_U^@) :} => color(green)(E_V^@ > E_U^@ > E_Y^@)
So, if you have a standard electrode potential table listed from most positive to most negative, you'll get
V^(2+) + 2e^(-) rightleftharpoons V, E_V^@
U^(3+) + 3e^(-) rightleftharpoons U, E_U^@
Y^(3+) + 3e^(-) rightleftharpoons Y, E_Y^@
So, to summarize, you now know that
-
V^(2+) can oxidize anything lower and to the right of the equilibrium, in your case U and Y.;
-
U^(3+) can oxidize anything lower and to the right of the equilibrium, in your case Y;
-
Y^(3+) cannot oxidize anything higher and to the right of the equilibrium, in your case V.
