Question

Question #e121a

Answer 1

You will be left with `1/128` of the original sample.

Explanation:

A radioactive isotope's nuclear half-life tells you how much time must pass before the half of the original sample undergoes decay.

In your case, the half-life of iodine-131 is 8 days. This means that any sample of iodine-131 that undergoes decay will be halved after 8 days, halved again after another 8 days, halved again after another 8 days, and so on.

You know that the fuel rods are stored underwater for 56 days. You can use this value to determine how many half-lives will pass.

`"no. of half-lives" = n_"half" = t/t_"1/2"`, where

`t_"1/2"` - the half-life of the element.

Plug in your values to get

`n_"half" = (56cancel("days"))/(8cancel("days")) = 7`

So, if the initial amount gets halved with every passing half-life, you can write

`A(t) = A_0/2^(n_"half")`

In your case, you have

`A(t) = A_0/2^7 = 1/128 * A_0`

This means that the fraction remaining after 56 days will be

`A(t)/A_0 = (1/128 * cancel(A[0]))/cancel(A[0]) = color(green)(1/128)`

Answer 2

1/128 remains

Explanation:

The first thing to do is count how many half lives have elapsed.

The half life (`t_(1/2)` )is the time taken for half the amount of a given sample to decay.

You can see that 56 days is 7 half lives since 56/8 = 7

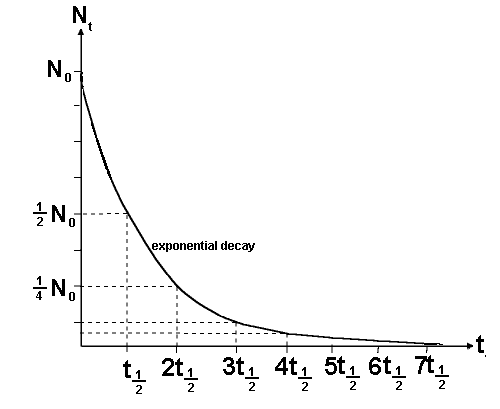
To get the fraction remaining we need to x by 1/2 seven times:

1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 = 1/128

If you don't get nice numbers like this you can use the equation for radioactive decay:

`N_t=N_0e^(-lambdat)`

`N_t` = no. atoms remaining

`N_0` = initial no. atoms

`t` = time elapsed

`lambda` = the decay constant.

We get the decay constant from the half life:

`lambda=(0.693)/(t_(1/2))`

`lambda = 0.693/8=0.0866d^(-1)`

Taking natural logs`rArr`

`ln((N_t)/(N_0))=-lambdaxxt=-0.0866xx56=-4.851`

From which `(N_t)/(N_0)=0.00782`

To compare this with the other method we can check the value of 1/128 = 0.00781 so that agrees quite nicely.