Question

Question #75aa3

Answer 1

(1) : The Angle btwn. tgts. is `arc tan2.4`

(2) : The tgts. intersects at pt. `(13/4,1/2).`

Explanation:

Eqn. of the Circle `S : x^2+y^2-y-3=0.`

To find the eqns. of Tangents, (tgts.) say `t_1 and t_2,` to `S` at the

points (pts.) where `x=1,` we have to first find the co-ords. of these

pts. To this end, we put `x=1` in `S.`

`1+y^2-y-3=0, or, y^2-y-2=0 rArr y=2, y=-1. x=1," already."`

Hence, the pts. of contact of tgts. with `S` are, say,

`T_1(1,2), and, T_2(1,-1).`

Knowing that `dy/dx` gives the slope of tgt., diff.ing `S` w.r.t. `x`,

`S : x^2+y^2_y-3=0 rArr 2x+2ydy/dx-dy/dx=0`

`rArr dy/dx=(-2x)/(2y-1)`

`:." Slope "m_1" of "t_1" at "T_1(1,2)" is "m_1=[dy/dx]_((1,2)=-2/3.`

`"Slope "m_2" of "t_2" at "T_2(1,-1)" is "m_2=[dy/dx]_((1,-1)=2/3.`

Hence, the Angle btwn. them`=arc tan|{(m_1-m_2)/(1+m_1m_2)}|`

`=arc tan|(2/3+2/3)/(1-4/9)|=arc tan2.4.`

To find, the tgts.' pt. of int., we solve the eqns. of `t_1 and t_2.`

`t_1 : y-2=-2/3(x-1), and, t_2 : y+1=2/3(x-1)`

`t_1+t_2 rArr 2y-1=0 rArr y=1/2 rArr 1/2+1=2/3(x-1),...[because, t_2]`

rArr 3/2*3/2+1=x=13/4.#

`:. t_1 nn t_2={(13/4,1/2)}.`

Enjoy Maths.!

Answer 2

The angle formed between the tangents is approximately `67.38˚`. The tangents intersect at the point `(13/4, 1/2)`.

Explanation:

When `x = 1`, we have:

`(1)^2 + y^2 - y - 3 =0`

`y^2 - y - 2 = 0`

`(y -2)(y + 1) = 0`

`y = 2 or -1`

We now find the equations of these tangents, by finding the derivative. Use implicit differentiation.

`2x + 2y(dy/dx) -(dy/dx) = 0`

`2y(dy/dx) - dy/dx = -2x`

`dy/dx(2y - 1) = -2x`

`dy/dx= (-2x)/(2y- 1)`

The slope of the two tangents are;

`(-2(1))/(2(2) - 1) = -2/3` and `(-2(1))/(2(-1) - 1) = 2/3`

We now find their equations:

For line `A` with `(1, 2)` and `m = -2/3`

`y- 2 = -2/3(x- 1)`

`y - 2= -2/3x + 2/3`

`y = -2/3x + 8/3`

For line `B` with `(1, -1)` and `m = 2/3`

`y - (-1) = 2/3(x- 1)`

`y + 1 = 2/3x- 2/3`

`y = 2/3x - 5/3`

We now find the point of intersection between these two lines.

`2/3x - 5/3 = -2/3x + 8/3`

`4/3x = 13/3`

`12x = 39`

`x = 13/4`

`y = 2/3(13/4) - 5/3 = 13/6 - 5/3 = 3/6 = 1/2`

Therefore, the point of intersection is `(13/4, 1/2)`. The next step is to complete a triangle using the lines and a line opposite the angle opposite the point of intersection.

Point `A`: `(13/4, 1/2)`

Point `B`: `(1, 2)`

Point `C`: `(1, -1)`

We now find the distances between each point.

`d_(AB) = sqrt((2 - 1/2)^2 + (13/4 - 1)^2) = sqrt(9/4 + 81/16) = 3/4sqrt(13)`

`d_(BC) = sqrt((2 - (-1))^2 + (1 - 1)^2) = sqrt(9) = 3`

`d_(AC) = sqrt((-1 - 1/2)^2 + (1 - 13/4)^2) = sqrt(9/4 + 81/16) = 3/4sqrt(13)`

Therefore, this is an isosceles triangle. We now find the measure of angle `theta` using the the law of cosines.

`costheta = (AB^2 + AC^2 - BC^2)/(2 * AB * AC)`

`costheta = ((3/4sqrt(13))^2 + (3/4sqrt(13))^2 - 3^2)/(2 * 3/4sqrt(13) * 3/4sqrt(13)`

`costheta = (90/16)/(9/8(13))`

`costheta = 10/26 = 5/13`

`theta ~~ 67.38˚`

Here's a graphical depiction of what's going on here:

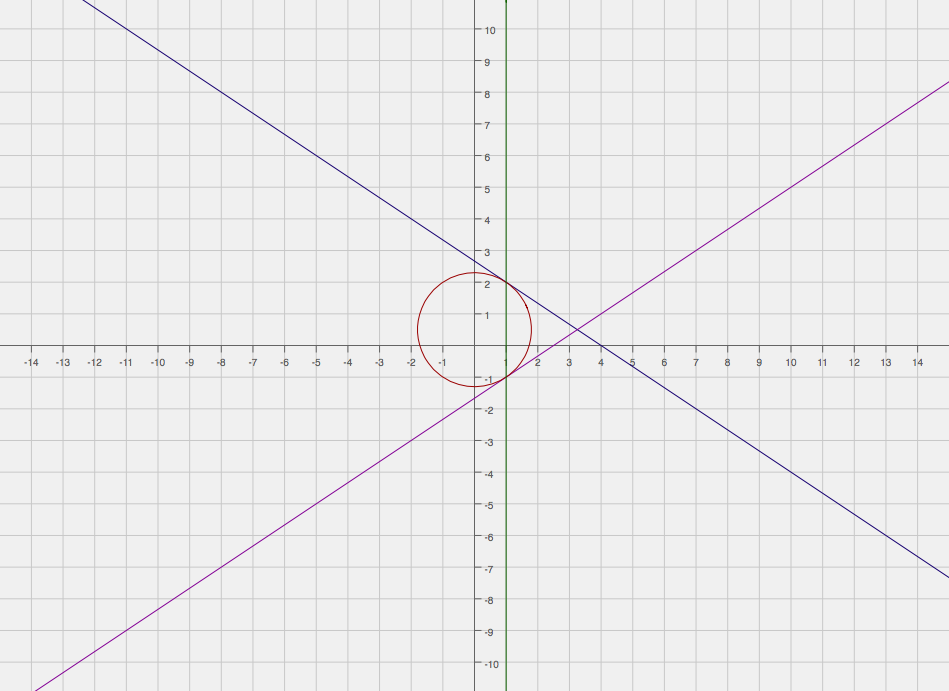
Hopefully this helps!